 This week in London the Thalesians hosted a presentation by Pat Hagan titled ‘Arbitrage free SABR‘. Knowing the popularity of Pat’s presentations, I had planned to arrive early to ensure I had a good seat, unfortunately I mis-calculated how long it took to get from the City to Canary Wharf, and so I arrived on time, and although I secured a seat, it was right at the back with terrible viewing angle.
This week in London the Thalesians hosted a presentation by Pat Hagan titled ‘Arbitrage free SABR‘. Knowing the popularity of Pat’s presentations, I had planned to arrive early to ensure I had a good seat, unfortunately I mis-calculated how long it took to get from the City to Canary Wharf, and so I arrived on time, and although I secured a seat, it was right at the back with terrible viewing angle.
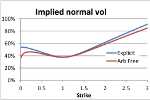
The main thrust of his presentation was, as the title suggests, to deal with regions where the classic asymptotic formula breaks down and admits arbitrage, mainly in the low strike region. He also covered ‘sub-models’ for negative and near-negative regions, as well as important aspects of hedging with SABR model.
His idea to fix the arbitrage problem was to concentrate directly on the probability density function, which yielded a numerical solution by finite differences rather than analytic formula. This is not a completely new idea, others have approached the probability density function from a probabilistic and PDE perspective. Two useful earlier papers are ‘Effective forward volatility’ by Andreason and Huge and ‘No-arbitrage SABR’ by Doust. There is a third paper, which I have not seen yet, by Balland and Tran called ‘Normal expansion of the SABR model‘, it is to appear in Risk Magazine.
All of these fixes require a higher degree of sophistication to implement than the original classic SABR formula. I can’t help but wonder if the SABR model was first presented without an analytic approximation, and only as the numerical solution of a PDE, would it have become as popular as it now is?

Gatheral presents the idea of SVI-SABR in http://mfe.baruch.cuny.edu/wp-content/uploads/2013/01/OsakaSVI2012.pdf