 In January a new approach to the SABR model was published in Wilmott magazine, by Hagan et al., the original authors of the well-known SABR model. They review some of the weaknesses of the model, and concentrate on the problem of negative probabilities induced by the original approximation formula, especially at low strikes.
In January a new approach to the SABR model was published in Wilmott magazine, by Hagan et al., the original authors of the well-known SABR model. They review some of the weaknesses of the model, and concentrate on the problem of negative probabilities induced by the original approximation formula, especially at low strikes.
To solve the problem they focus on the probably density function, similar to the approach taken by Andreason and Huge, ZABR – Expansions for the Masses. They find a solution which agrees closely with the original SABR formula but corrects the possibility of negative probabilities. The solution however is not an analytic formula, but a one-dimensional PDE which can be solved numerically using finite difference techniques.
When implementing one will encounter two problems which can be resolved;
Problem 1
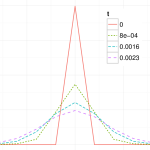
Crank-Nicolson can lead to spurious oscillation depending on the geometry of the finite difference grid (specifically the Courant Number).
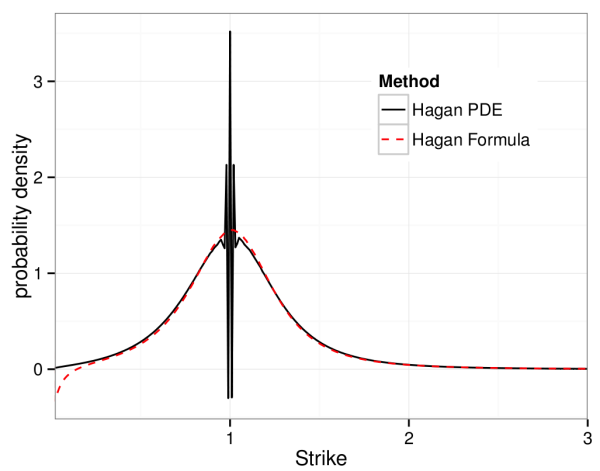
A solution is to use alternative finite difference schemes, the TR-BDF2 and Lawson-Swayne schemes work well on this problem, and provide fast stable solutions.
Problem 2
The underlying rate variable \(F\) may require a large number of points in the discretisation for longer dated options. This problem is not new and can be remedied by a change variable, as suggested in the well-known Anderson-Piterbarg book (p. 292 section 7.4).
$$z(F)=\int\frac{dF’}{D(F’)}$$
These ideas have been written up in a more formal document, Finite Difference Techniques for Arbitrage Free SABR, Le Floch and Kennedy, Jan 2014.
