- “An industrial solution” – provides computation to near machine precision for option prices over an extremely large range!
- Fast and analytic in nature, employs rational polynomials to determine implied BpVol.
- Follows the Bachelier model; that is, dF = σdW.
A new method for computing implied BP Vol (basis point volatility) analytically has come to light. It is described by Le Floc’h, “Fast and Accurate Analytic Basis Point Volatility”, June 2016, he relies on four rational polynomials to produce his highly robust “LFK-4” approximation. The approach improves on the algorithm of J. Choi, K Kim and M. Kwak (2009), “Numerical Approximation of the Implied Volatility Under Arithmetic Brownian Motion”.
The Choi routine for determining the implied volatility works reasonably well but truly pales in comparison to the LFK-4 representation when accuracy is considered, especially for far out of the money options. It must be noted however that this is justified, the purpose of Choi’s method is to facilitate practical implied volatility calculations, whilst Le Floc’h designs his algorithm in the spirit of Jackel’s paper; “Let’s be rational”, November 2013, where his approach through Black’s volatility produces a wide range of highly accurate solutions well beyond the realm of normal option trading.
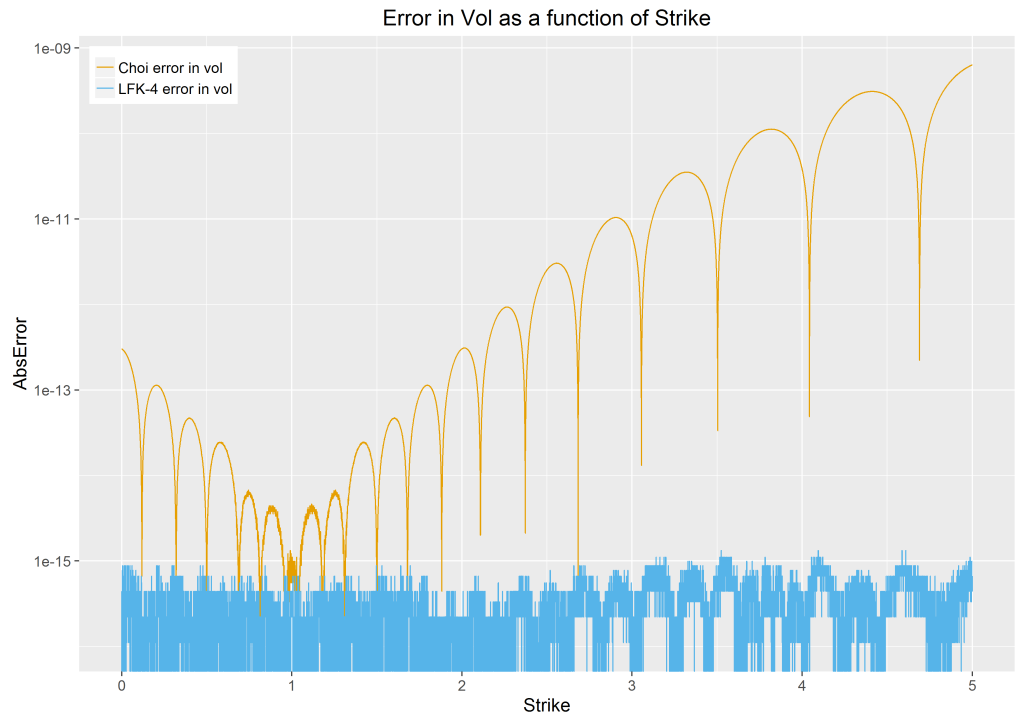
Setting normalized values of forward and maturity to 1.0, figure 1 demonstrates just how powerful the LFK-4 approximation is with the absolute error in volatility being driven right down to near machine precision for the standard computer. The approach remains stable when computing implied volatility for any option price which is machine representable.
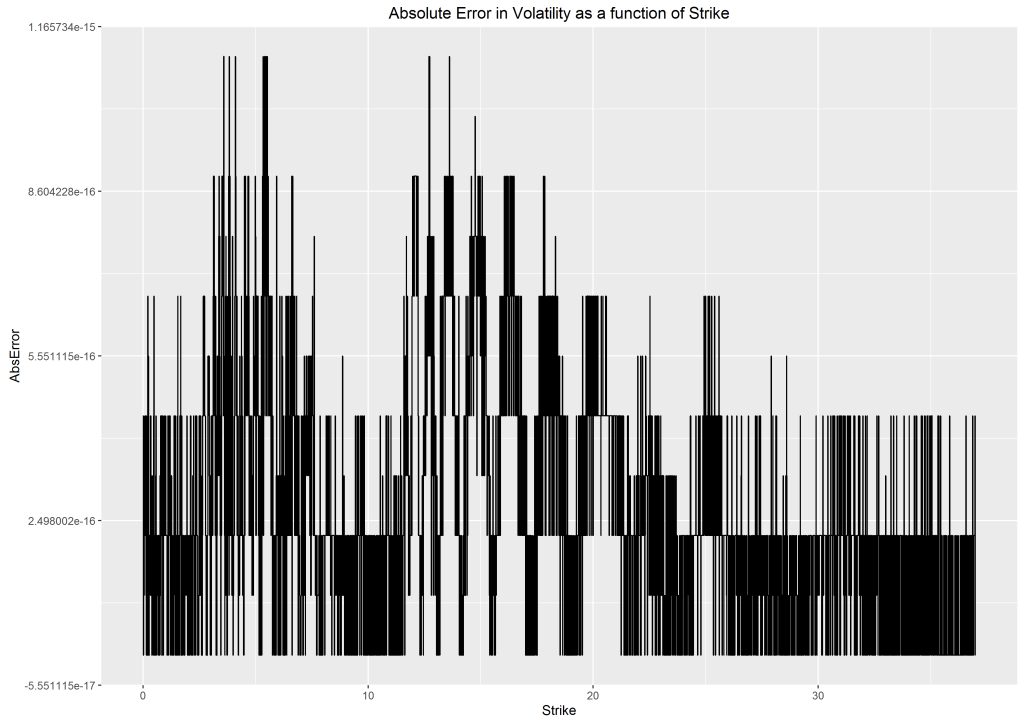
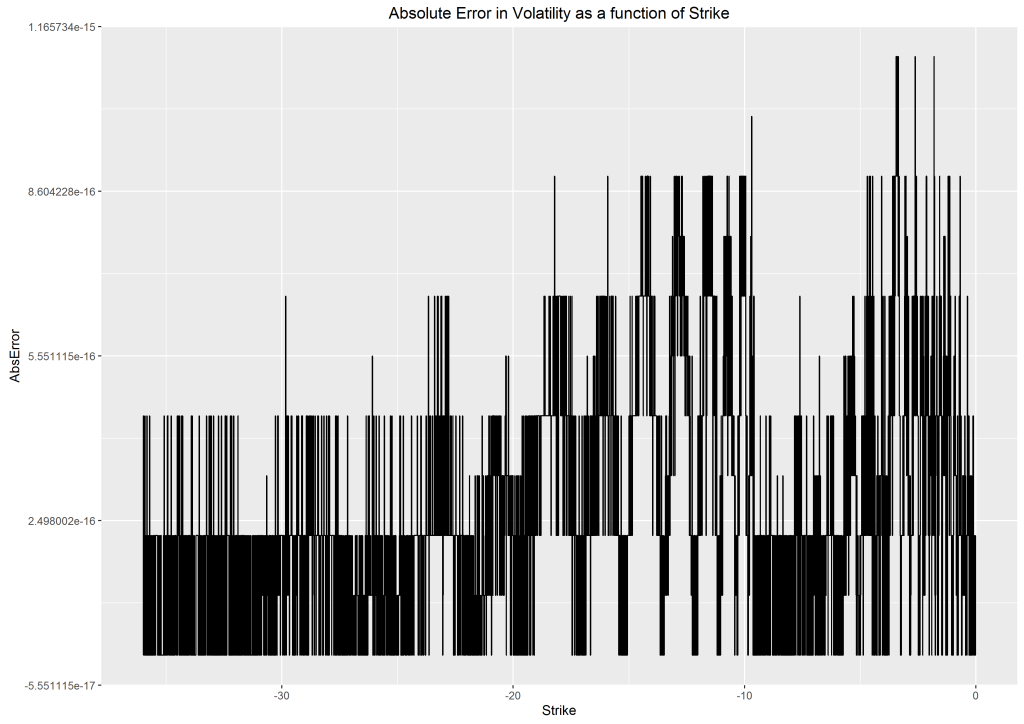
Figures 2 and 3, representing call and put options respectively, illustrate this; the absolute limits on these graphs is due to the limitation of the normal distribution function factored in our test cases.
Finally, it is important to note that the computation speed for this approach does not deteriorate from that of the Choi implementation, in fact it is approximately three times as fast! Thus in all respects, the Le Floc’h method is the superior algorithm.
This article is authored by Eoin O’Hare.
Update 15th Nov. 2016
The paper “A note on the equivalence between the Normal and Lognormal implied volatility: A model free approach” by Cyril Grunspan characterises the time value of an option, under the normal model, in terms of the incomplete gamma function, leading to a completely analytic implied bpvol, provided one can invert the incomplete gamma function quickly!
Update 8th Nov. 2017
Peter Jackel has recently published a paper with a similar goal, “Implied Normal Volatility”, July 2017, Wilmott.
