Authored by, Serena Manti and Gianluca Molteni of the Financial Engineering and A.I. team at List.
In this post we would like to introduce our paper “Parsimonious HJM-FMM Model with the New Risk-Free Term Rates“, a modified version of the Heath-Jarrow-Morton (HJM) model that addresses the limitations of the traditional approaches in the context of the upcoming LIBOR transition. We propose a new method for incorporating the new risk-free term rates (RFRs) into the HJM model, which is crucial for modelling interest rates in a post-LIBOR world.
The standard HJM model is a popular tool for pricing derivatives. It assumes that the term structure of interest rates is determined by the current short-term interest rate and its expected path. However, in the post-LIBOR world, the term structure of interest rates will be based on the new risk-free reference rates, which are expected to replace LIBOR as the benchmark for a wide range of financial products. These new rates are overnight rates, contrary to the LIBOR that is characterised by a term structure.
The possibility to build a term structure also for the RFRs allows to extend the traditional LIBOR Market Model (LMM), strongly related to the old rates, to a new framework called Forward Market Model (FMM – Lyashenko and Mercurio, 2019a, 2019b and 2019c). The FMM is able to simultaneously describe the evolution of both the forward-looking (LIBOR-like) and the new backward-looking term rates using the same stochastic process for both. It is due to note that, when switching from forward-looking to backward-looking rates, the properties of the standard interest-rate modelling framework are not only maintained but also enriched. The new rates, in fact, own all the relevant analytical features held by the LIBOR, needed for pricing vanilla derivatives such as swaps, caps/floors and swaptions.
Our novel HJM model is specifically designed to exploit the potentialities of the new RFRs. That’s why we call it HJM-FMM model. Its originality resides in that it is built as a combination of two different models: the FMM model of Lyashenko and Mercurio and the parsimonious HJM model of Moreni and Pallavicini, 2014. However, it goes beyond the two because it demands a much lower computational effort (due to a reduced number of parameters) with respect to the first one and, contrary to the second one (built using the old LIBOR), all the structures generated inside it start from a single rate, the RFR.
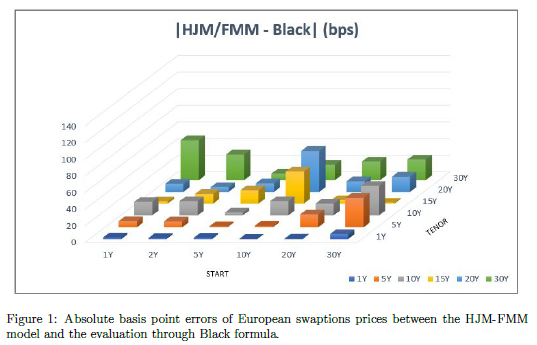
In the paper we demonstrate the effectiveness of our model by comparing the results obtained to those coming from other commonly used interest rate models, including the Black model and the Hull-White model. We show that our model can be used to price a wide range of interest rate derivatives, including caps, swaptions and Bermudan swaptions, both on the new RFRs and on the old LIBOR rates.
For those interested in the full paper, please click here.
