The year-end turn-rate (or the turn-of-the-year rate) is the interest rate for the period between the last business day of the year until the first good business day in the next year. For example, in the US the 2014 turn rate is the interest rate for the period between 31-Dec-2014 until 2-Jan-2015. The rate can be substantially different than normal levels of interest rates, apparently because of pressures around the end of year reporting period. As Stephen Aikin notes in his post on the subject, pre-GFC end of year rates would be substantially higher due to illiquidity, a longer-than-average lending period and the desire to bolster balance sheets with cash for reporting purposes. These pressures have substantially reversed in recent times as central banks became increasingly cognizant of funding stresses and their possible negative contagion effects.
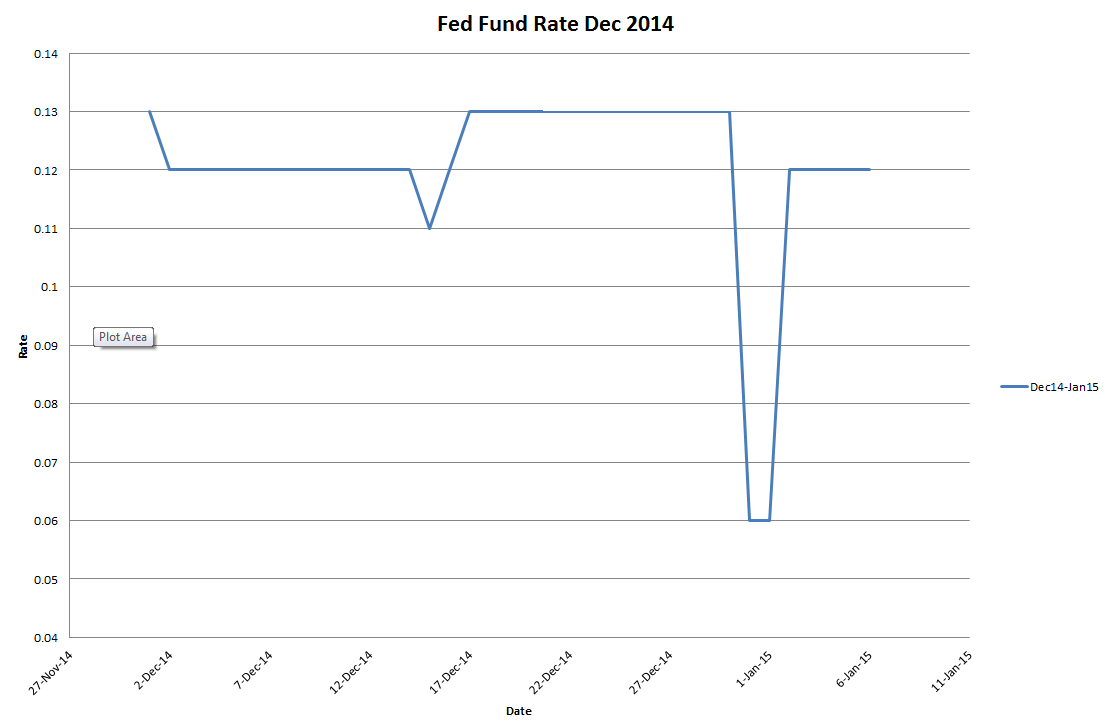
Whatever the reason, the effect is clearly seen in the Fed Fund rate over the year end, the graph below shows a turn rate of 6bp, whilst the average rate around the year end was just under 13bp, a spread of almost -7bp.
A similar jump can be noticed in recent years, as seen in the table below. The effect is much less pronounced than it once was, in the mid-80s the turn rate had a spread of more than 500bp!! A classic paper on this topic is One Good Turn, by Galen Burghardt and Susan Kirshner, RISK Magazine, November 1994.
| Year | Avg Around Turn | Turn Rate | Turn Premium | Turn Ratio |
|---|---|---|---|---|
| 2009 | 0.12 | 0.05 | -0.07 | 0.43 |
| 2010 | 0.18 | 0.13 | -0.05 | 0.71 |
| 2011 | 0.07 | 0.04 | -0.03 | 0.56 |
| 2012 | 0.17 | 0.09 | -0.08 | 0.53 |
| 2013 | 0.08 | 0.07 | -0.01 | 0.88 |
| 2014 | 0.13 | 0.06 | -0.07 | 0.48 |
I happened upon this year’s turn rate when investigating a MTM reconciliation issue between CHARM and an in-house system when valuing short dated OIS swaps beginning just at the year end. Thanks to the drop in the Fed Fund rate and the short dated nature of the trades, we spotted that the in-house system was picking up the wrong fixing on certain days. Without realising the possibility of the year end effect, one quite naturally might think the fixing itself was incorrect, as it is so different to the neighbouring rates.
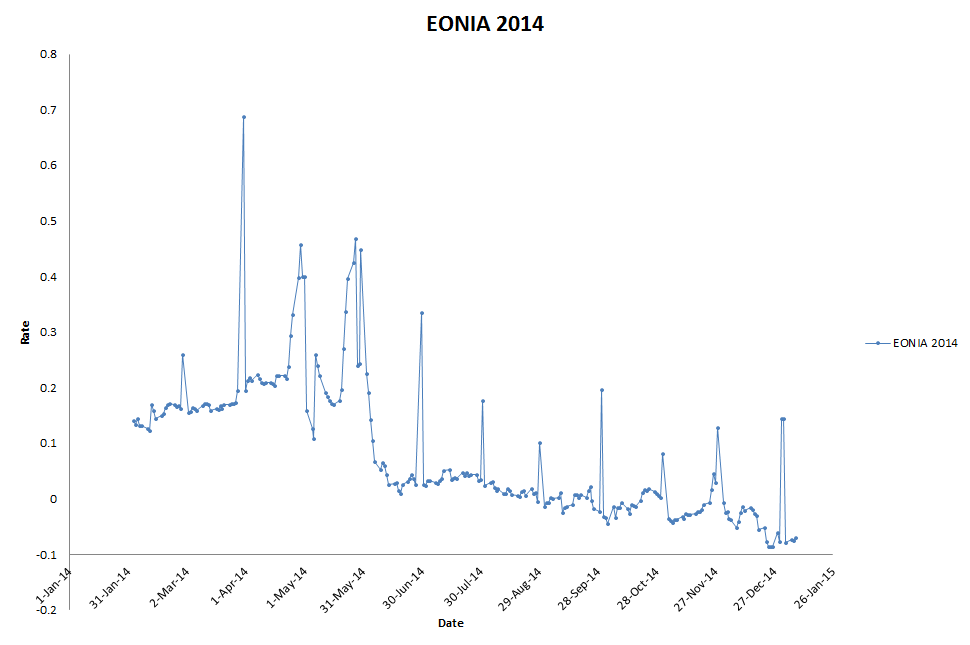
EONIA ‘Hearbeat’
The year end effect is not just confined to USD rates (nor to the year-end!). One can very clearly see both quarter-end jumps and month-end jumps in the EONIA rate during 2014. Historically, Eonia has also seen significant jumps at the start (and end) of ECB maintenance periods. This has been referred to as the Eonia “heartbeat” and has been ascribed to both a preference of banks to front-load their reserve requirements, and also banks squeezing liquidity of those needing to meet their reserve requirements at the end of a maintenance period. With maintenance periods now longer following the ECB’s change to a six-week meeting schedule, it will be interesting to see whether these spikes are now smaller than previously.
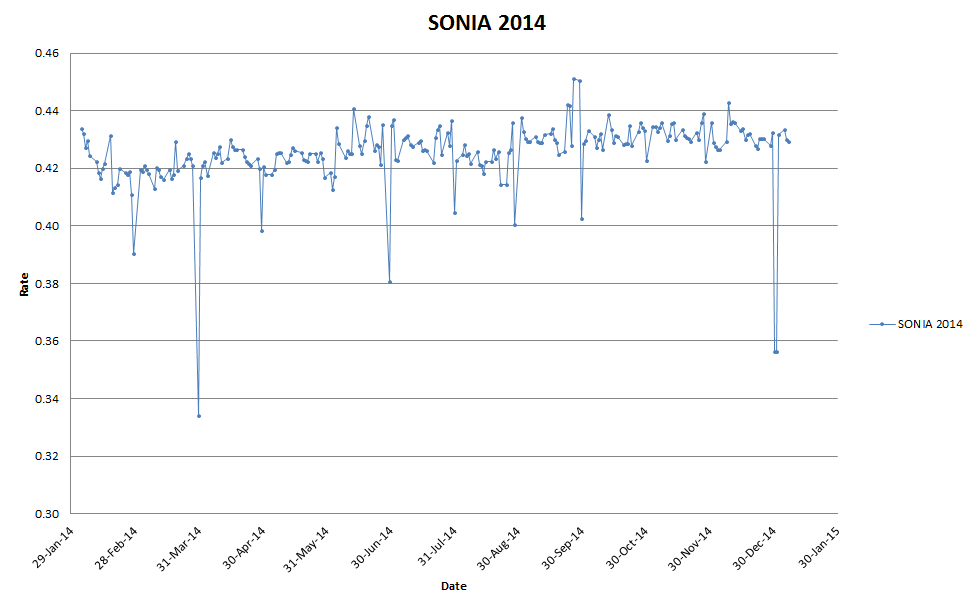
GBP Turn Rates
In GBP the effect is much less pronounced, consider the 2014 SONIA rates, one can see some effects at quarter ends.
Curve construction
The observation of jumps in certain rates has implications for curve construction. Modern curve construction methods have a focus on smooth (instantaneous) forward rates, yet given the evidence of turn rates, one is compelled to find a way to estimate the size of the jump and to allow smooth interpolators to avoid such jumps. The detection of the size of the jump is mainly based on ideas in the paper of Burghardt and Kirshner, whereby they identify an instrument containing the turn period, and neighbouring rates which do not, and assume the difference between the average rate implied by the neighbouring instruments and the instrument covering the turn period is explained only by the jump. A excellent recent paper on the topic is
EONIA Jumps and Proper Euribor Forwarding by Ferdinando M. Ametrano and Paolo Mazzocchi. Ametrano’s recent papers on curve construction make explicit mention of jumps and are certainly worth reading, for example, Bootstrapping the Illiquidity by Ametrano and Bianchetti.