Indices are the best way to calculate compound interest

• To avoid complications with compound interest calculations, administrators of RFRs could publish a single Index each day.
• The equivalent term rate for any period could then be calculated by looking up the index level from the start date and the end date of each period. Interim rates do not need to be known.
• This allows for a golden source of Index publication and fallbacks to be embedded within the Index calculation itself.
• This approach has a precedent in the Chilean Peso (CLP) swaps market.

Compound Interest Problems

With reference to the possible demise of ‘IBOR indices, and the rates that might replace them, I hear a lot of concerns from people about how to handle compound interest for overnight rates.

This seems to be such a hot topic in SONIA markets that the Bank of England has issued “calculator specifications” to aid the uptake of SONIA and compound interest via the Infrastructure Forum.

It is also evident in CHF SARON, where SIX (the benchmark administrator of SARON) have recently issued no less than 6 calculators for different approaches to a compound calculator.

Importantly, both the BoE and SIX recognise that in the event of a LIBOR fallback, we could have multiple “old” LIBOR periods ending on the same day, as shown below:

This means that benchmark administrators cannot publish a single rate each day (per tenor) to act as the equivalent simple term interest rate for a compounded overnight rate.

Fortunately, there is another way.

Read on to find out about how Chilean swaps trade as vanilla IRS even though they are based on a compounded overnight rate. The approach is very similar to Total Return Swaps, so this isn’t something new.

The simplest way forward for Rates markets would be to adopt these same market conventions. And to forget about compounding OIS trades completely.

Chile Camara Index

The whaaaaaaaat?!

As part of our work on RFRs, we have recently extended our currency support in CHARM to include the Chilean Peso, CLP.

Swaps in CLP trade against the Camara Index, or specifically the Chilean Average Chamber Index (“Indice de Camara Promedio” or ICP Rate).

It turns out that the ICP is pretty ingenious.

From the BSEF filing for CLP-ICP swaps:

“The reference rate for the floating leg of the swap is the ICP Rate, which represents the cost of funds resulting from financing a position at the overnight rate (one day), using the TIB (Interbank Average Interest Rate). The TIB rate is published on a daily basis by the Central Bank. If the Central Bank does not publish the rate, the calculation will be based on the Monetary Policy Rate.”

Calculation of ICP Rate, Bloomberg SEF

How to Use an Index

You would not be alone in the world if you thought, at first glance, that this looks like a total nightmare. Why is it different to every other Rates market convention?

But then you speak to a quant and they point out:

I think such an index is a very slick idea, very efficient for pricing and simple to use. Coupons are value of the index at the end of the coupon divided by the value at the start, scaled appropriately by the notional. No fiddly stuff on fixings on individual trades.

Dr Gary Kennedy, ClarusFT October 2018

I didn’t really understand Gary’s point until I started doing the calibration work on GBP Fallback Spreads for my blog “LIBOR Fallbacks – What will the GBP spread be?“.

What I found is that if I calculated the value of the index on any arbitrary date, I could calculate ALL interest amounts for ANY combination of dates simply by looking up the value of the index. This isn’t rocket science, but it is a beautiful aspect of linear mathematics.

A Spreadsheet to calculate any Index values for RFRs

To help everyone looking into the implementation of LIBOR fallbacks, and also generally looking at how to deal with compound interest calculations, it will probably help if I lay out the spreadsheet I used. We know that readers found the equivalents very helpful when looking into ISDA SIMM.

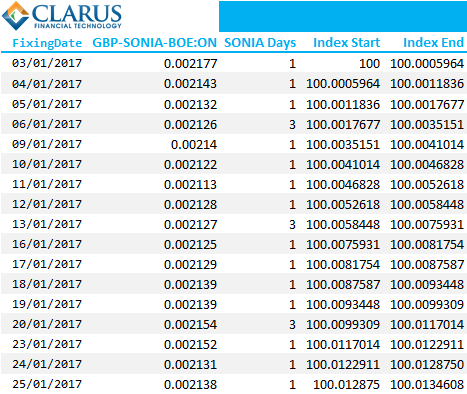
To get this right, you must understand the dates that the overnight index applies to. This is why I’ve made the Index Start and End so explicit in the above. The calculation for the Index End is simply:

\( \tag {1} I_{T+1} = I_{T0} . (1 + R . \dfrac{Days}{365})\)

where;

I = Index value
R = Overnight RFR rate
Days = Number of days that the rate is applicable for (e.g. on weekends an “overnight” rate applies for three calendar days).
365 = Day count convention for the RFR in question. The above example is using SONIA which uses a “365-Fixed” convention.

From Index to Simple Interest Rate

The reason that these indices are so powerful is that we only have to look up the start and end value of the index itself to calculate the equivalent simple interest rate between those two dates. We do not need to bother with compounding. We do not concern ourselves with the individual overnight fixing rates between the dates.

Because this might not be obvious to everyone (it certainly wasn’t obvious to me), I’ve chosen to layout this point below and show you the step-by-step calculations that I followed in Excel. Feel free to follow along…

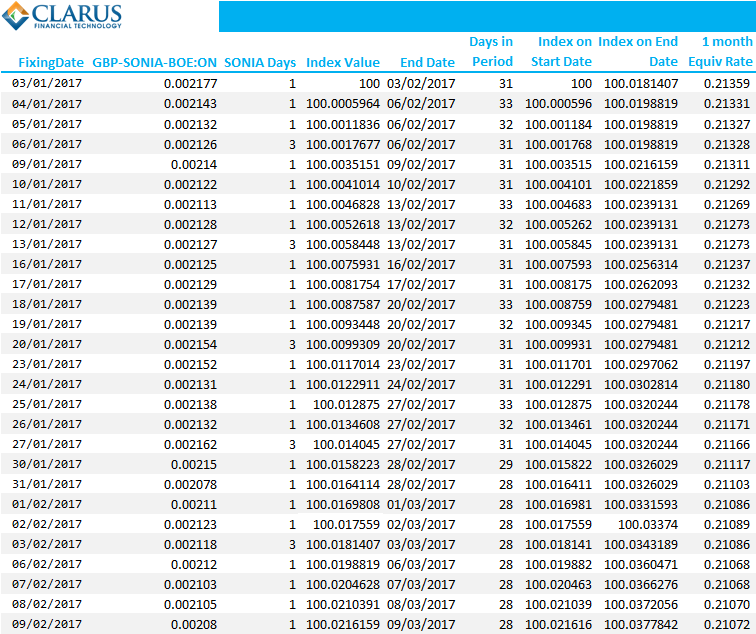
Showing;

• The value of the SONIA index for each day from 3rd January 2017.
• The first one month period runs from 3rd January – 3rd February.
• To calculate the equivalent term rate for that one month period, we simply take the index value as of 3rd Jan and the index value of 3rd Feb.
• The calculation is then:

\( \tag {2} R_{1month} = \dfrac{365}{Days}.(\dfrac{I_{T2}}{I_{T1}} -1)\)

where;

I = Index value
Days = Number of days in the term period
365 = Day count convention for SONIA.

Inserting the values from the Excel table shows the calculation completely:

\( \tag {3} R_{1month} = \dfrac{365}{31}.(\dfrac{100.0181407}{100} -1)=0.21359\% \)

Why Indices Are So Good – A Summary

In Summary;

• We present the methodology to use Indices to calculate equivalent term interest rates for compounded overnight RFRs.
• Publishing an index level each day has a precedent for compounded interest rates in the Chilean Peso swaps market.
• Publishing an index value each day means that only the start date and end date index values need to be known.
• The benchmark administrator can be in charge of index publication, creating a “golden source”.
• The index calculation can embed within it a fallback mechanism itself (e.g. the CLP-ICP index falls back to the Monetary Policy Rate in the event of publication problems).
• And I leave the last words to Dr Gary Kennedy:

Suppose we are in the middle of a coupon period, so some overnight rates are known and some are not.
With an index, you would just need current value of the index and the value at the start of the coupon, which is much less fiddly than iterating over the daily fixings.

Dr Gary Kennedy, October 2018