- We describe how to calculate Margin Valuation Adjustments under ISDA SIMM™.
- This is a simple four step process starting with Risk Projection and IM calculation.
- And concluding with present valuing the margin costs.
- We then compare the MVA adjustments for both cleared and uncleared swaps.
What is a Margin Valuation Adjustment (MVA)?
As Amir stated back in May this year;
MVA arises when Initial Margin is required on a Derivatives trade….and is an adjustment for the funding cost of IM. [W]e are not just interested in the IM today, but over the life of the trade.
There are some excellent papers and books linked in Amir’s original article which are well worth a read.
How do we calculate MVA?
To calculate MVA under ISDA SIMM™, we need four pieces of information:
- Risk Profile of the swap – not just today but also projected forward in time.
- The Initial Margin calculated as per ISDA SIMM associated with this risk profile at each point in time.
- The discount curve as at today.
- The cost of financing the Initial Margin. This is typically expressed as a margin over the discount curve being used.
This blog will demonstrate how we use this 4-step process to arrive at a Margin Valuation Adjustment for a standalone Pay Fixed 10 year USD IRS under ISDA SIMM.
Step One – Risk Profile
CHARM is our real-time margin and risk management tool. Pardon the gratuitous use of YouTube above – I realise that some of our clients will have this video hidden behind firewalls. But I do think it’s pretty cool that I can type in “Pay $50m 10y” and produce my what-if trades. We also have some natural language processing within this text string, which will overcome typos and certain nuances. You can even type a bit of broker slang with “Mine 10 years” if you feel like it….no Alexa link yet though.
CHARM also provides a Forward Scenario of risk, producing a grid that shows the risk at a number of points in the future – see below:
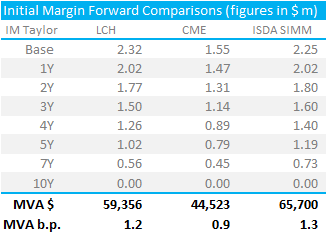
Showing;
- The risk profile of our 10y USD Swap today and at several points in the future
- The left most column shows the risk at it stands today on the USD 3m Libor index. As expected, most of the risk is in the 10 year bucket.
- The risk vertices that we are using on the curve are the same as defined under ISDA SIMM. This means that we don’t have to bother with any risk transposition in our spreadsheets.
- In the 5y column, we can see that the trade has effectively decayed into a 5y swap, with just $25k DV01 still outstanding in 5 years time.
- This Forward Scenario rebuilds the curves in forward space, hence realising the forwards of the trade and replicating any fixings. When we look at the discounting risk on the USD Fed Funds curve, we see a small amount of risk as well.
Step Two – ISDA SIMM™ Calculator
We will now combine our analysis from CHARM with the ISDA SIMM in Excel calculator that we built a month ago. We simply copy and paste each of the columns in turn into the Excel spreadsheet:

- We copy and paste the risk at 1y, 2y, 3y, 4y, 5y, 7y and 10y forward points in time
- This should give us enough granularity to compute MVA across the life of the swap, allowing for changes in risk profile and risk weightings within ISDA SIMM.
Step Three – Discount Curve as at Today
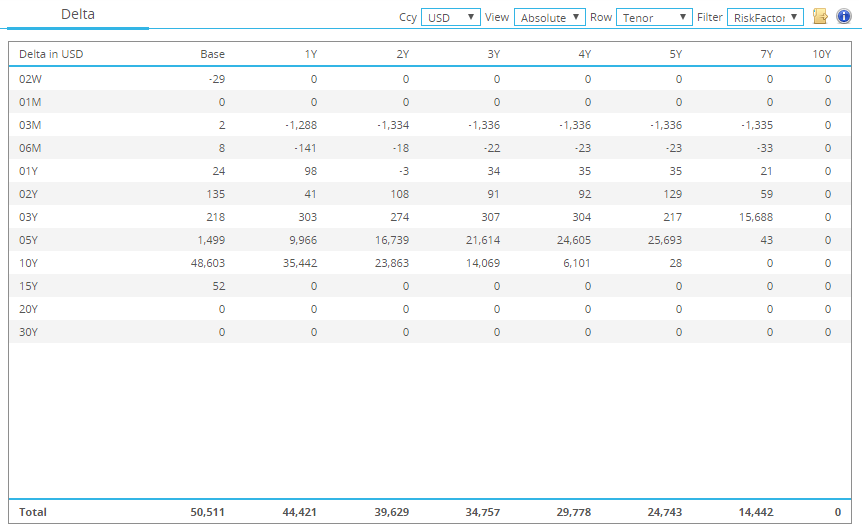
Whilst we are concerned with how IM evolves over the lifetime of our swap, we are still calculating MVA according to the state of the market today. Therefore, we need to know what our discount curve looks like right now. CHARM allows us to export daily discount factors for our curves, giving us perfect granularity:
Step Four – MVA Calculation
Finally, MVA is calculated as:
\( \ MVA = \sum\limits_{t=0}^{T} InitialMargin * Margin Rate * df_{t+1} * \frac{Days}{365} \)
Where;
Initial Margin is calculated at discrete points in time according to the projected delta profile of risk at that point in time.
Margin Rate is defined as our cost of raising funds over the risk free discount rate. Here, we are using 50 basis points over Fed Funds.
\( {df_{t+1}}\) is the discount factor at time t+1.
Comparing the MVA
Using the above calculations, we can plot the IM profile of a standalone 10 year USD swap at LCH, CME and bilaterally under ISDA SIMM:
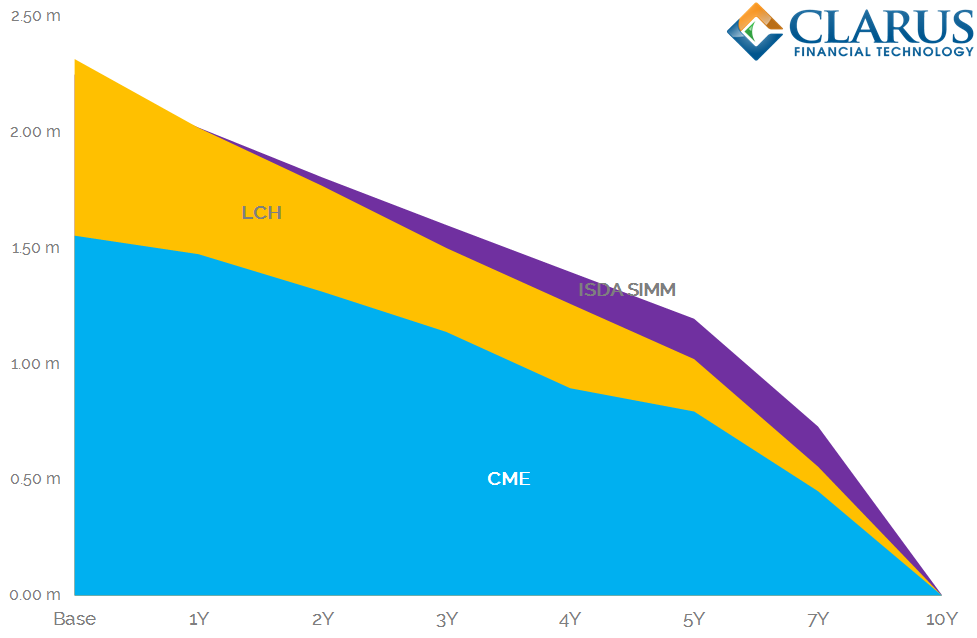
When we calculate the MVA for these three charts, it is equivalent to calculating the area under each of the three plots. These amounts are shown in the table below, which remember are for a standalone pay-fixed 10 year USD Swap in 50k DV01.
Showing;
- MVA is highest under ISDA SIMM.
- As we talked about previously, however, the standalone difference between a cleared swap and a bilateral swap are not as high as we might expect.
- It is most interesting to note that the initial “base” value for IM is higher at LCH than under ISDA SIMM. There are several caveats here remember – IM is not symmetrical at CCPs, and of course CCPs can multi-laterally net all of your trades together. Notable, nonetheless.
- IM decays quicker at LCH than under ISDA SIMM. This means that over the life of the swap, more IM is required bilaterally than at LCH.
- MVA is significantly larger than the bid/offer spread when we assign a cost of 50 basis points to Initial Margin.
In Summary
- We provide a step-by-step guide to calculating MVA for uncleared swaps
- This sheds more light on a potentially opaque practice of valuation adjustments in the market
- Our methodology is transparent and can be replicated
- This blog concentrates on the methodology. Future blogs will look in more detail at the differences between margin in cleared and uncleared applications.
- From this initial analysis, we already see some interesting relationships between cleared and uncleared margin to investigate. Remember to subscribe to keep up to date with our findings.