- The ISDA SIMM™ methodology has been expanded to include Cross Currency Swaps.
- We explain in detail how to create the required input sensitivities.
- These sensitivities are not the typical cross currency basis risk that a risk management system would calculate.
- Once the input sensitivities are calculated, the calculation of Initial Margin follows the typical SIMM equations.
- We show how these can be implemented in Excel.
- UPDATE: We now offer free 14-day trials for our SIMM for Excel product
Effective April 1st 2017, version R1.3 of the ISDA SIMM™ methodology has now been published. This introduces Cross Currency risk into the Delta Margin calculations for Interest Rate risk. So long as you can calculate your appropriate risk sensitivities, the implementation is straight-forward.
Cross Currency Swaps are Special Under the UMRs
Before we get into the margin calculations, we need to remind ourselves that physical FX products without optionality are exempt from the Uncleared Margin Rules. A cross currency swap could theoretically be split into a physical FX transaction and an accompanying series of interest rate payments. This would exempt the FX leg of the transaction (and it’s associated FX risk) from Initial Margin.
The ISDA SIMM model recognises this fact, therefore exempts the physical exchanges of notional from the input sensitivities. This is explained in detail in this document.
Fixed Notional Swaps
At first pass, that document may appear a little daunting. However, most types of Cross Currency swap have a known notional. In this case, the treatment is simple:
Whilst simple, it does have some significant implications:
- We are left with a coupon swap. For a floating-floating swap this will now have the following risks:
- Interest Rate Risk to each floating index across the maturity profile of the swap
- FX risk equal to the present value of each stream of coupons
- A very small amount of cross currency basis risk equal to the discounting risk
- Compare this with the risk profile of a floating-floating swap that does not have the principal exchanges removed:
- No interest rate risk (other than fixing risks in the first period)
- A very large FX risk equal to the notional amounts once the initial exchange has occurred
- A large amount of cross currency basis risk in the final maturity bucket
- Furthermore, this treatment can reduce the implied interest rate risks. For example, the interest rate risk components of a Fixed-Fixed cross currency swap with initial and final exchange will be reduced significantly (by around 90% depending on the level of the coupons).
Resettable Cross Currency Swaps
People familiar with the interdealer market will be aware that market participants trade a specific structure – one with an FX-Resetting principal. Much of the ISDA documentation is given over to these Resettable (or Mark-to-Market) cross currency swaps. This is only fair, given that the interbank market will make up the lion’s share of outstanding positions between counterparties currently in-scope for the UMRs.
The subsequent step-by-step screenshots from Excel show how we generate the input sensitivities for these structures.
1. Input Sensitivities
I consider a 5 year, spot starting EUR-USD cross currency swap with FX Resets.
First, I build a generic cross currency pricer. To do this, I pull market data into Excel. The discount factors (“df’s”) are simply calculated as 1/(1+r), where r is the zero coupon rate for the period, derived from compounding the (serial) 3-month forwards together. The zero coupon rates for the €/$ basis curve are the EUR IRS curve plus the basis:
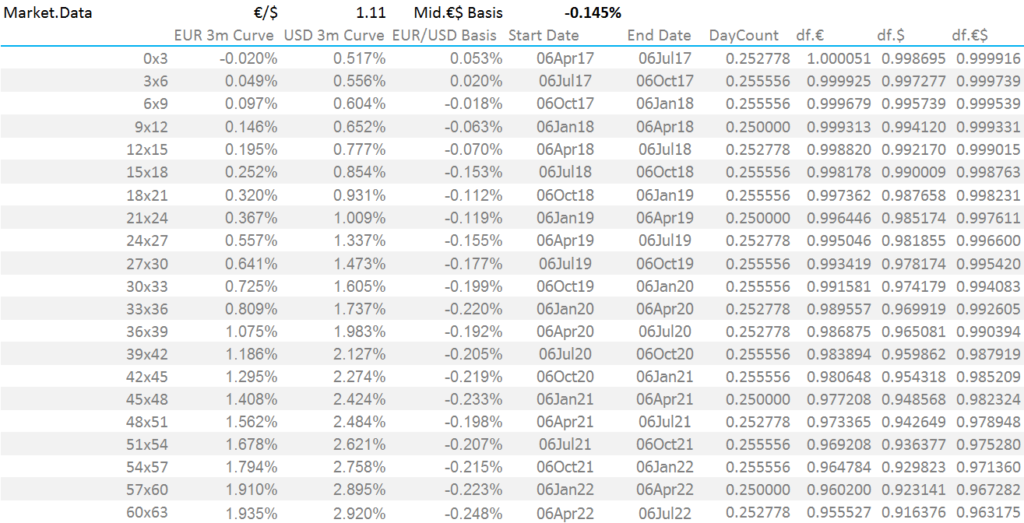
Secondly, we generate the cashflows for a Resettable Cross Currency Swap on the EUR side. Note that the EUR notional stays constant for the life of a resettable cross currency swap:
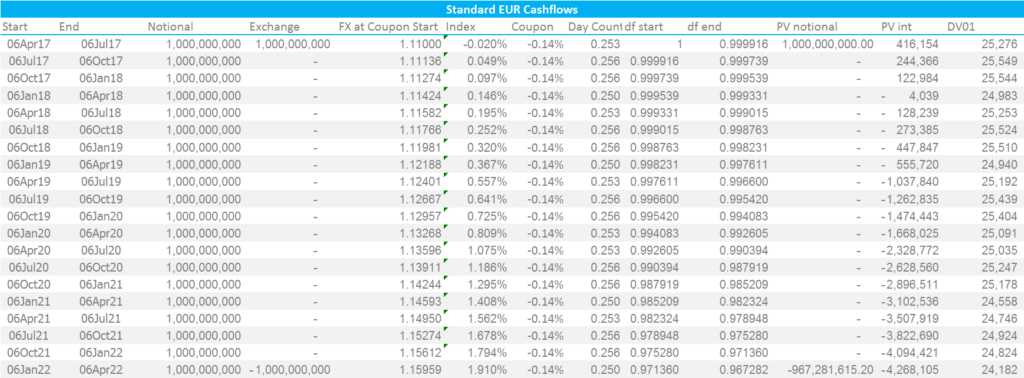
The PV columns (Present Values) are calculated using the discount factors at the beginning of the period (initial notional) or the end of the period (final notional plus all interest flows) multiplied by the cashflow on each date. The total PV of this leg is the sum of all values in the columns “PV Notional” and “PV Interest”.
The “FX” rates are now forecast for each coupon payment date. This is calculated as Spot FX * df(€$)/df($).
Next, we generate the cashflows for the USD leg. This leg has a variable USD notional amount that “resets” to the prevailing FX level every 3 months. The Notional amount is hence forecast as EUR Notional * FX at each coupon payment date.
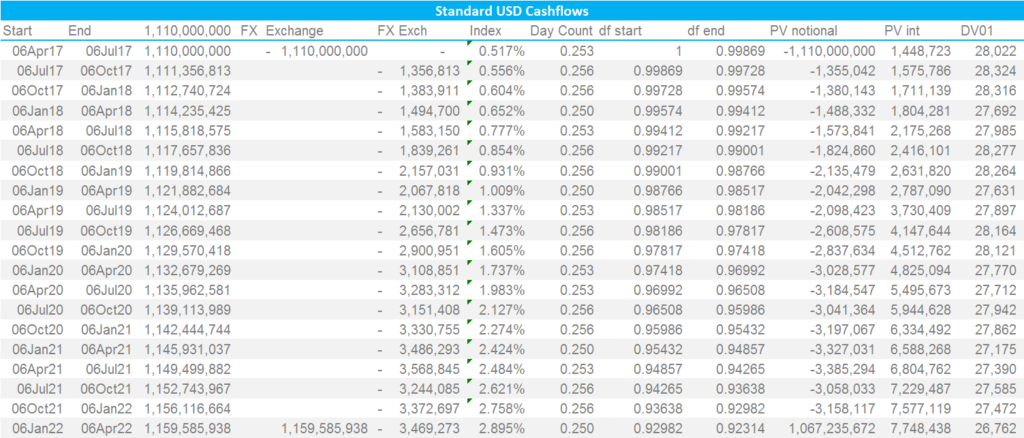
Please note;
- The PVs are calculated using the discount factors at the beginning of the period (initial notional and FX Exchanges) or the end of the period (final notional plus all interest flows) multiplied by the cashflow on each date. The total PV of this leg is the sum of all values in columns “PV Notional” and “PV Interest”.
- We are discounting at USD Libor 3m. Therefore, by definition the total of “PV Notional” plus “PV Interest” must be zero at all times. Check your spreadsheeting if that does not hold!
ISDA SIMM expects only a single input vector for Cross Currency basis risk. This means that we apply a single parallel shift to the basis curve to calculate our risk exposure. This is achieved in my spreadsheet by replicating the market data and applying a single shift:

Next, we must modify the cashflows. ISDA states that we remove the known cashflows, whilst leaving the unknown amounts in place. In practice, we therefore push the initial exchange forward from spot to 3 months forward:
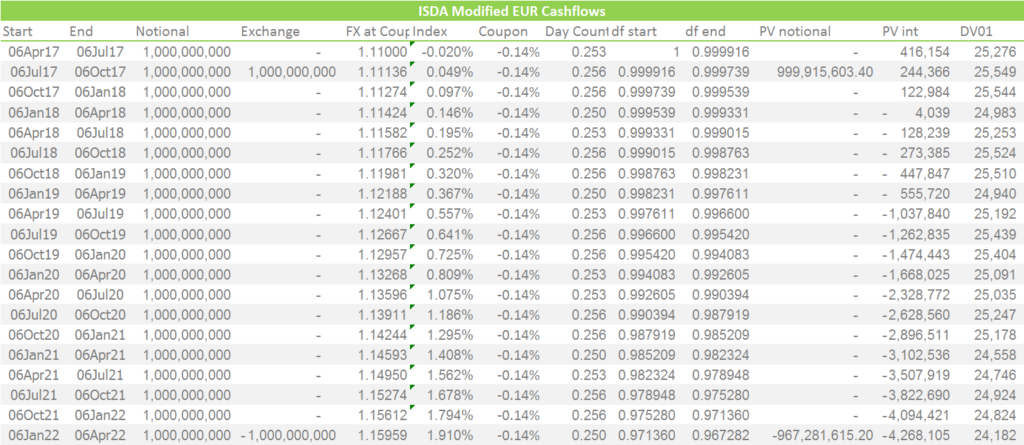
Showing;
- Assuming that we already know the fixing rate for the first exchange, we must therefore push the exchange of notionals forward to the next coupon date.
- In our example, our €1bn is now theoretically received on the 6th July instead of 6th April.
And similarly on the USD side;
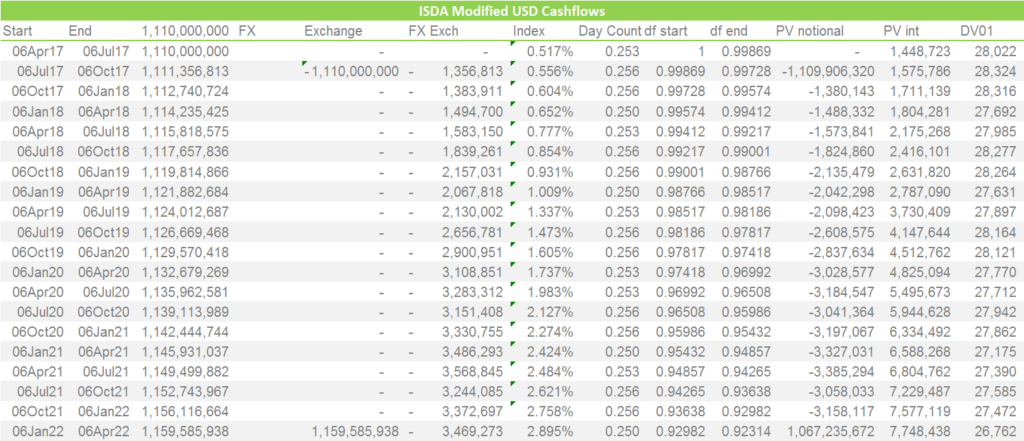
- Note that we use the forecasted USD notional of $1,111,356,813 as the “new” initial exchange amount value 6th July.
- Again, the PV of all flows after the first coupon period should sum to zero due to the use of USD Libor discounting.
To calculate the input sensitivity for ISDA SIMM, we just need to perform a trivial piece of spreadsheeting:
- Sum the PVs of both structures into a USD-equivalent amount (using the defined spot FX in market data of 1.11).
- Replicate the cash-flows of both structures but use the modified market data to do so.
- Sum the PVs using the modified market data into a USD-equivalent amount (using the defined spot FX in the modified market data of 1.11).
My results:
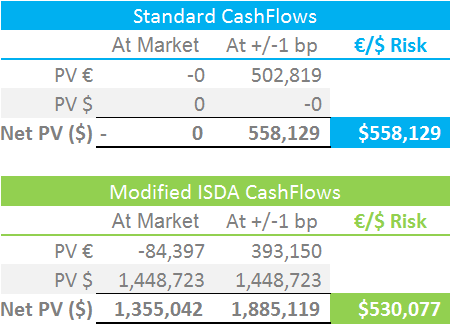
- The Input Sensitivity for ISDA SIMM is $530,077 for our 5 year €/$ Resettable Cross Currency Swap example.
- This is the change in value of the modified swap structure caused by a 1 basis point parallel shift of the cross currency basis curve.
- If we did not modify the cashflows, this at-market swap would have a cross currency basis risk of $558,129.
- We can see that the difference in risk is consistent with removing the first period cashflows. We are effectively treating this first period as an FX Forward instrument (minus the interest!).
- The treatment adds some “noise” to the risk calculations. We now have a small PV in both EUR and USD, even for an at-market trade that is discounted at 3m USD Libor.
- In reality, this is of small concern. Given that all of these trades will be discounted at OIS anyway (mainly USD), then we would not have zero PVs in the “real world” of swap trading anyway.
- In practice, these modified cashflows have removed almost all of the FX “delta” that would otherwise be present once we move past the initial exchange date.
That concludes our in-depth look at how to create the input sensitivities. The treatment is particularly effective for Resettable Cross Currency Swaps. The one thing that I don’t understand is why we do not replicate this for fixed notional swaps. Why not just add back-in the initial notional amounts from the next coupon date? That would seem more consistent to my mind. Otherwise, a “hedged” position of resettable versus non-resettable cross currency swaps will consistently create input sensitivities under ISDA SIMM.
2. Risk Weightings
Armed with our input sensitivities, we can now move forward at lightning pace to calculate IM (well, if you have implemented any of our previous ISDA SIMM blogs you can!).
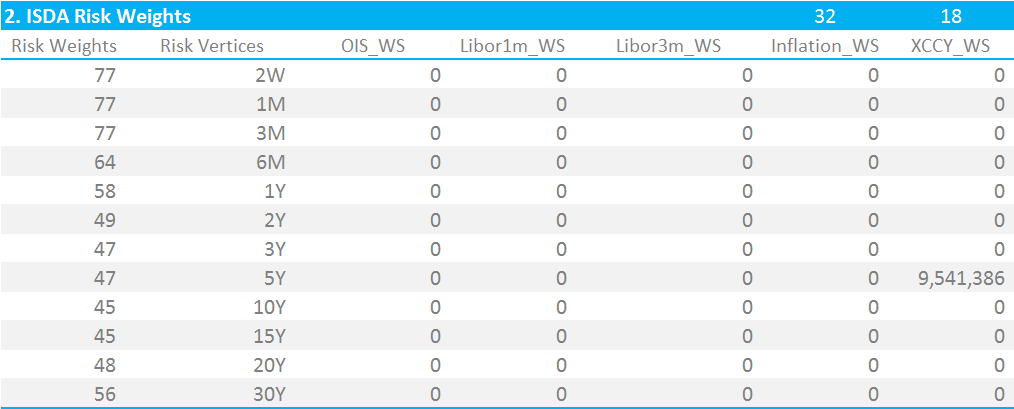
Showing;
- Risk Weights for EUR IRS in the left column, which vary by tenor.
- Columns for exposures to OIS, 1m and 3m Libor plus Inflation and Cross Currency.
- Both Inflation and Cross Currency exposures under ISDA SIMM use a single risk-weight for the entire curve. The risk weight for Cross Currency is 18. This is considerably lower than IRS weights for regular currencies and more typical of the calibration to the low-volatility IRS currency (JPY).
- I have bucketed my input sensitivity for Cross Currency into the 5 year bucket. We can choose any single tenor for all input sensitivities for Cross Currency, but do ensure there is only one tenor populated.
- To stay consistent with previous ISDA SIMM calculators in Excel, I have retained the same formatting and lay-out. This makes subsequent calculations easier.
3. Correlations
 Implementing Cross Currency basis exposures is akin to introducing a new “sub-index” into my original ISDA SIMM Excel calculator. However, rather than using the sub-index correlation matrix, ISDA has calibrated a standalone cross currency correlation vector. To make the spreadsheeting easier, I implement this as a single column matrix (shown to the right), with the value of 18% repeated for each tenor.
Implementing Cross Currency basis exposures is akin to introducing a new “sub-index” into my original ISDA SIMM Excel calculator. However, rather than using the sub-index correlation matrix, ISDA has calibrated a standalone cross currency correlation vector. To make the spreadsheeting easier, I implement this as a single column matrix (shown to the right), with the value of 18% repeated for each tenor.
4. Calculate Cross Currency Initial Margin
Once again, we must implement the below formula into Excel:
\( \tag {1} K = \sqrt{\sum\limits_{i,k}{WS_{k,i}^2+{\sum\limits_{i,k}}{\sum\limits_{(j,l)≠(i,k)}{φ_{i,j}{ρ_{k,l}}{WS_{k,i}}{WS_{l,j}}}}}}\)Breaking this formula down into its’ constituents shows that;
\( {WS_{k,i}}\) is the input sensitivity to the cross currency basis curve at a given tenor multiplied by the ISDA-supplied risk weighting. In Excel, it is easiest to implement this as an array the same size as the underlying IRS exposures.
\({φ_{i,j}}\) is the correlation of the “WS” terms between indices (i.e. between index i and index j in the nomenclature). ISDA deem that the Libor 1 month Index has a correlation of 98.2% with the Libor 3 month Index, and they have calibrated that these indices have an 18% correlation with cross currency basis. This applies across all currencies and across all tenors for the underlying IRS exposures.
\({ρ_{k,l}}\) is the correlation of the “WS” terms from one tenor to the next (i.e. between tenors k and l in the nomenclature). Because cross currency basis is calculated as a single exposure across the whole curve, we do not need this for standalone cross currency calculations. However, I would be loathe to remove from a spreadsheet calculator as we will undoubtedly have some cross currency trades that have IRS risk in two currencies, across different maturities, as well as their cross currency basis risk.
From the above equation, it should be clear that the Delta Margin will collapse to just the WS term for a single Cross Currency exposure – in this example, $9.54m. It is therefore more instructive to consider a cross currency exposure versus the same IRS exposure:
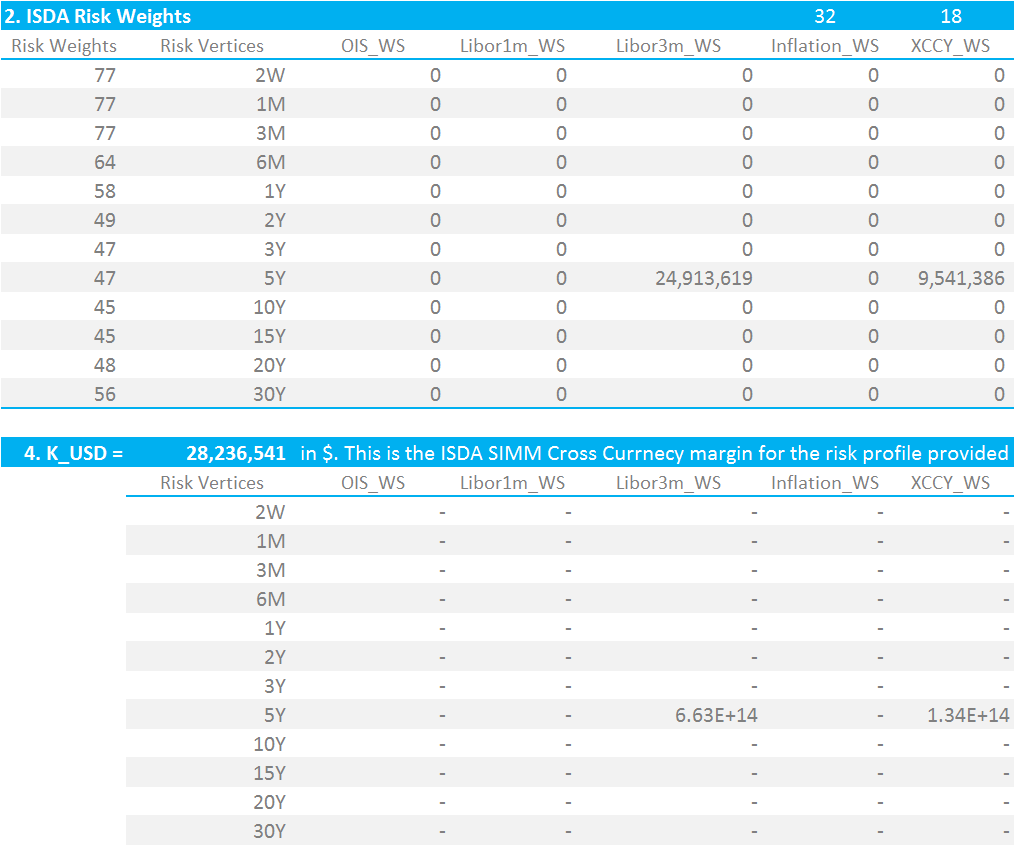
Showing;
- Each exposure has an 18% correlation to the other.
- In effect we are squaring each WS term, and then adding in WS(1)*WS(2)*18%.
- I find it easiest in Excel to implement these using a SUMPRODUCT formula.
- Each cell in the bottom matrix takes the WS term above it, squares it, and adds in the sumproduct of the other WS terms and the appropriate correlation matrix.
- It is important to note that all exposures have an 18% correlation with the Cross Currency WS value.
Finally
As keen followers of the blog will be aware, ISDA also has implemented Concentration Thresholds in the latest versions of the model. It is important to note that, whilst Inflation exposures contribute to this threshold, cross currency basis exposures are ignored.
Our series of ISDA SIMM blogs is very popular. Remember to subscribe to stay updated for more.
UPDATED: We now offer free 14-day trials for our SIMM for Excel product.

