ISDA SIMM™: Concentration Thresholds

January 31, 2017 by No comments
  • Concentration Thresholds are introduced as part of Version 1.2 of ISDA SIMM™ as of 4th February 2017.
  • We must derive our own co-variance matrix between currency pairs in order to implement the new concentration thresholds into our ISDA SIMM Excel calculator.
  • We provide a step-by-step guide that builds on our previous explanations of the model.
  • UPDATE: We now offer free 14-day trials for our SIMM for Excel product.

4th February 2017

Version 1.2 of ISDA SIMM™ comes into effect as of 4th February 2017. The new technical requirements document can be found on the ISDA website. The biggest change is the calibration of Concentration Thresholds. I wrote a blog entitled “ISDA SIMM™: Multi Currency Portfolios”, and flippantly stated:

\( {g_{bc}}\) is calibrated according to Concentration Risk in each currency. This is yet to be implemented by ISDA, so we can ignore this term for the time being.

That is no longer the case. So let’s see how we go about implementing Concentration Risk into ISDA SIMM™.

A Delta Scalar?

From a brief overview of the requirements, I thought it would be a simple case of adding a look-up table to my input sensitivities. However, the complexity exists on the multi-currency side when combining deltas across more than one currency.

So let’s start simple and build from there.

1. Risk Weightings

All of our blogs have used the concept of Risk Weight*Sensitivity to arrive at our inputs to the model – the Weighted Sensitivities.

ISDA has now calibrated the Concentration Thresholds. We therefore apply a multiplier (CR), which is the Concentration Risk Factor per currency. As per the documentation, this is defined as:

\( \tag {1} CR_{b} = max \Bigg(1,\bigg(\frac{|\sum\limits_{k,i}{s_{k,i}|}}{T_{b}}\bigg)^{1/2}\Bigg)\)

Meaning that we take the absolute value of the sum of all of our deltas in each currency and divide them by \( {T_{b}}\). We take the maximum of either the square root of this term, or 1.

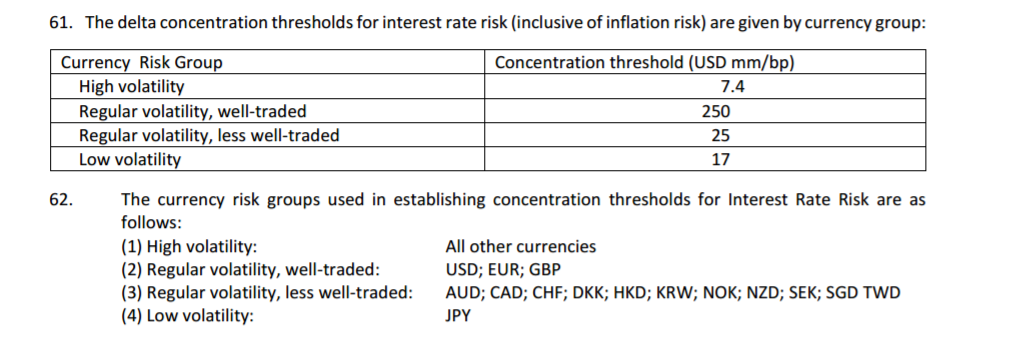
ISDA has calibrated \( {T_{b}}\) for each currency according to the table below:

ISDA SIMM Concentration Thresholds

It is important to note that:

  • We need to apply these thresholds at a total delta level – i.e. across all indices (including Inflation) for a given currency.
  • This means that we calculate one \( {T_{b}}\) per currency, according to the look-up table above.
  • This is the trivial part of the exercise. The interesting part is when we combine Concentration Thresholds across multiple currencies.

My ISDA Sensitivities now look like this:

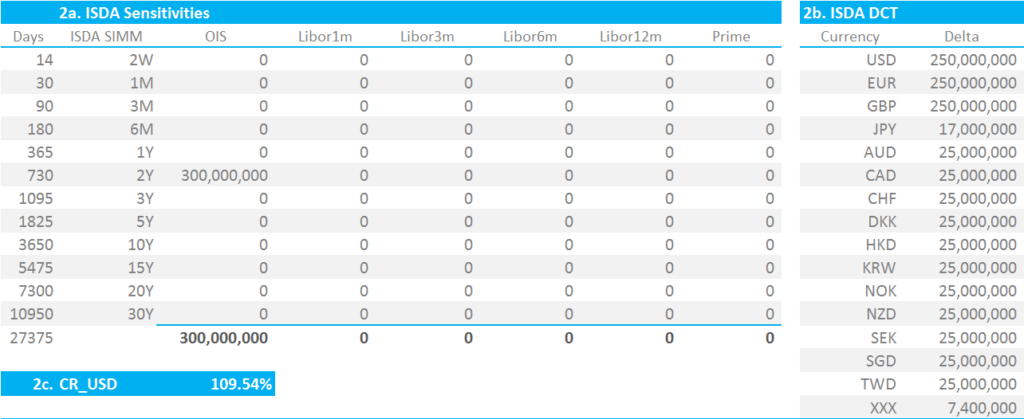
ISDA Sensi2
Introducing the CR Concentration Threshold multiplier to our input Sensitivities

Showing;

  • 2a. ISDA Sensitivities are our Delta inputs before any multipliers
  • 2b. ISDA DCT is a Delta Concentration Threshold (DCT) look-up table to check whether the sum of our delta across the grid in “2a” are over the threshold.
  • 2c. is the new term that we are introducing “CR_XXX”, with XXX being the 3 letter currency code. Our total delta is $300m of DV01 (huge!), which is over the threshold for USD. This means that our multiplier for all deltas is nearly 10% (109.54%).
  • To calculate the ISDA SIMM Delta Margin for a single currency (K_USD), we now simply proceed by multiplying all of our input deltas by 109.54%, as per the below equation:
\(\tag {2} {WS_{k}=RW_{k}s_{k}CR_{k}}\)

i.e. Risk Weight*Sensitivity*Concentration Risk.

  • Because we love examples, this means the following. A DV01 sensitivity of $300k 2y in paid USD Swaps creates a margin amount of $14.7m.
  • This amount is linear until the threshold. A DV01 of $300m in 2y USD Swaps creates a margin amount of $16.103bn.

2. Multiple Currencies

Recall from our earlier blog that to calculate Delta margin across multiple currencies, we must apply the following equation;

\( \tag {3} DeltaMargin = \sqrt{\sum\limits_{b}{K_{b}^2+{\sum\limits_{b}}{\sum\limits_{(c)≠(b)}{γ_{bc}{g_{bc}}{S_{b}}{S_{c}}}}}}\)

Having learnt how to calculate “K” in our original blog, the “new” terms are:

\( {S_{b}}\) which is either the sum of all of the “Weighted Sensitivities” or the value of K for currency b. We first take the smaller of the sum of the WS’s and then the larger of this and  “negative K” for currency b. This means that \( {S_{b}}\) can, in some instances, be a negative number.

\( {γ_{bc}}\) is calibrated by ISDA. It is set at 27% according to the documentation here.

\( {g_{bc}}\) is calibrated according to Concentration Risk in each currency. It actually varies by currency pair, meaning we need to create ourselves a new covariance matrix.

3. Concentration Threshold Covariance Matrix

We must now calculate the values of \( {g_{bc}}\) for each possible currency pairing in our portfolio. The formula is given by ISDA as;

\(\tag {4} {g_{bc} = \frac{min(CR_{b},CR_{c})}{max(CR_{b},CR_{c})}}\)

Meaning;

  • We take all of those freshly calculated CR_XXX values for each currency and combine them into a covariance matrix.
  • Because we take the Max and Min of each currency, the covariance matrix is nice and symmetrical, providing a good litmus test for our spreadsheeting!

I choose to combine the \( {g_{bc}}\) and \( {γ_{bc}}\) terms within the single matrix to simplify the subsequent calculations.

Our newly derived co-variance matrix is shown below. I have chosen a 4 currency portfolio with a paid position of $300m DV01 in 5 years in each of 4 currencies (EUR, JPY, CNY and USD). This covers high volatility, well-traded regular volatility and low volatility currencies.

The size of the positions is a bit ridiculous, but I needed to go over the thresholds for all currencies whilst keeping it simple!

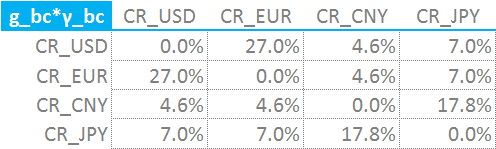
CR Covariance
The CR Covariance Matrix
  • This is the key take-away from this blog.
  • Recreating this covariance matrix, along with the previous multi-currency blog, allows us to implement Concentration Thresholds.
  • We now simply follow our tried-and-tested sumproduct formulas.

Our final calculation grid is shown below:

MultiCCY Calculation Grid
Multiple Currency Calculation Grid

Showing;

  • S_CCY is as per our previous definition of \( {S_{b}}\): either the sum of all of the “Weighted Sensitivities” or the value of K for currency b. We first take the smaller of the sum of the WS’s and then the larger of this and  “negative K” for currency b.
  • K_CCY is the delta margin for that currency.
  • Our “Calc” takes the square of K_CCY in each column. To this we add the sumproduct of the S_CCY row with the appropriate line on the CR covariance matrix. This sumproduct term is multiplied by S_CCY for the currency itself.
  • For example, the USD column is the sumproduct of all S_CCY terms with the line “CR_USD” of our covariance matrix. This sumproduct is then multiplied by the S_CCY term for USD.
  • Our final Delta Margin is the square root of the sum of all of the “Calc” terms.

In Summary

  • We walk through the new Concentration Risk Factors (aka Concentration Thresholds) in version 1.2 of ISDA SIMM.
  • This version of the model goes live on February 4th 2017.
  • The weighting of the input sensitivities is simple for a single currency portfolio.
  • We show how to derive the required covariance matrix to implement the model for a multiple currency portfolio.
  • The SIMM model has stayed true to its’ guiding principles of speed, transparency and ease of replication. This allows us to extend our Excel model to incorporate the new calibration.
  • UPDATE: We now offer free 14-day trials for our SIMM for Excel product.

Stay informed with our FREE newsletter, subscribe here.