- We look at Initial Margin under ISDA SIMM™ for multiple currency portfolios.
- ISDA SIMM includes a 27% correlation parameter for aggregating across different currencies.
- We find that the difference between margins in Cleared and Uncleared space depends on the risk profile.
- The differences range from 1% to 74%, with Uncleared Margin always higher.
- UPDATE: We now offer free 14-day trials for our SIMM for Excel product.
Multi Currency Rates Portfolios
Extending our ISDA SIMM Excel Calculator to include multiple currencies turned out to be a fairly trivial task – at least from an Excel standpoint. The equation that I had to interpret and implement this week was very similar to the ones we looked at last time:
\( \tag {1} DeltaMargin = \sqrt{\sum\limits_{b}{K_{b}^2+{\sum\limits_{b}}{\sum\limits_{(c)≠(b)}{γ_{bc}{g_{bc}}{S_{b}}{S_{c}}}}}}\)I will assume that our audience is a loyal one and hence already read the previous blog! If not, please head over here. Having learnt how to calculate “K” last time, our new terms this week are:
\( {S_{b}}\) which is either the sum of all of the “Weighted Sensitivities” or the value of K for currency b. We first take the smaller of the sum of the WS’s and then the larger of this and “negative K” for currency b. This means that \( {S_{b}}\) can, in some instances, be a negative number.
\( {γ_{bc}}\) is calibrated by ISDA. It is set at 27% according to the documentation here.
\( {g_{bc}}\) is calibrated according to Concentration Risk in each currency. This is yet to be implemented by ISDA, so we can ignore this term for the time being.
The Calculation
Conceptually, the calculation above is very similar to the ones we have performed previously to calculate ‘K’ in the first place. In Excel, my calculation grid looks like this:
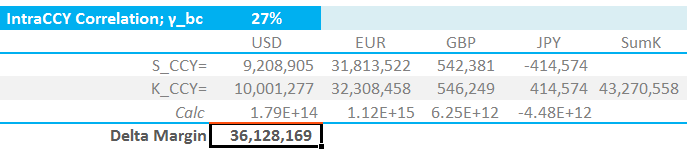
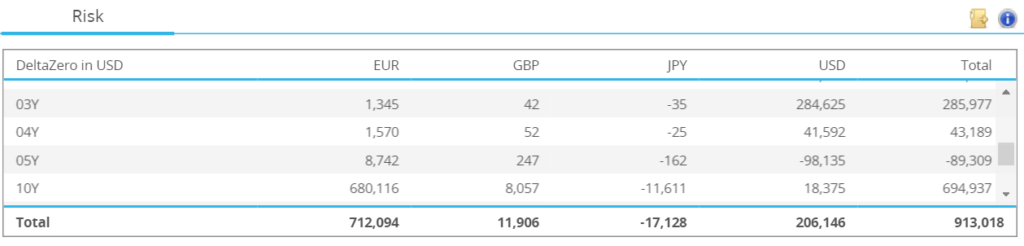
We’ll look at the portfolio of trades behind these numbers later in the blog. First of all, it is interesting to note that;
- We have here a “K” value for each currency, calculated as per our previous blog. If the portfolio were only one currency, this would be the IM of the portfolio.
- If we simply took the sum of all of these values, we’d have an Initial Margin of $43.27m for this portfolio (the “Sum K” column).
- However, ISDA SIMM™ acknowledges the offsetting nature of risks across currencies.
- In this case, we can see that the contribution of JPY is negative for the portfolio as a whole (the “S_CCY” row), where-as it would be positive if we only had JPY in the portfolio (the “K_CCY” row).
- Under ISDA SIMM, this portfolio has an Initial Margin requirement of $36.13m. This is considerably lower than a simple sum across all currencies of the individual “K” values, highlighting the offsetting nature of some of the risks.
The Portfolio
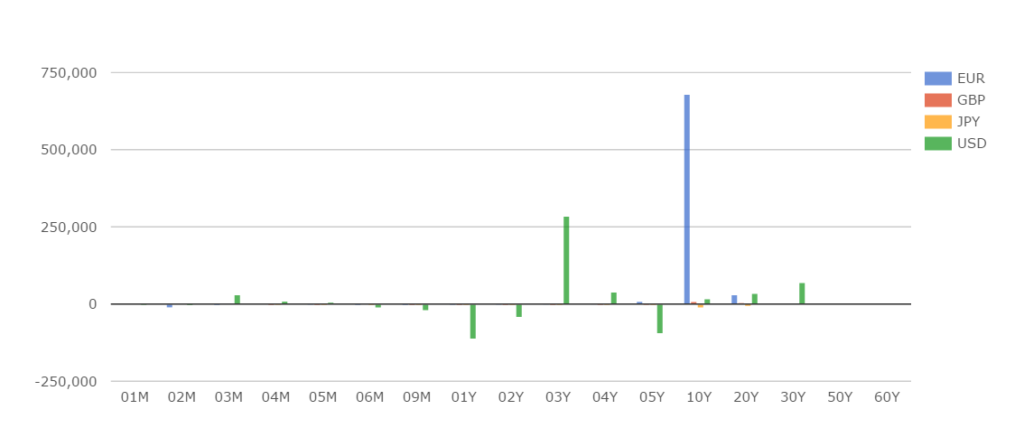
As a first pass, I wanted to look at a Rates portfolio that has risk in USD, EUR, GBP and JPY. This portfolio hence covers three “normal” currencies plus the lower volatility JPY. Using CHARM, I therefore exported the risk of a 118 swap portfolio, that has the below delta profile:
Showing;
- A decent-sized portfolio with over $900k in DV01 outright risk
- All the risk is expressed in USD-terms, split by currency
- The risk is mainly in 10y EUR rates with a paid position of $680k (the large blue bar)
- There is also significant risk in 3y USD rates with a paid position of $284k (the large green bar)
- The positions in GBP and JPY are very small compared to EUR and USD
Our methodology will be broadly equivalent to last week’s, meaning that:
- We first export the Delta Zeros from CHARM and then transpose these risk ladders into the requisite ISDA risk vertices.
- All risks are expressed in USD equivalent DV01s.
- We assume full collateralisation with a zero threshold. This means that the effect of any “FX Deltas” on the ISDA SIMM calculation is very small.
Comparing Margins for Cleared vs Uncleared
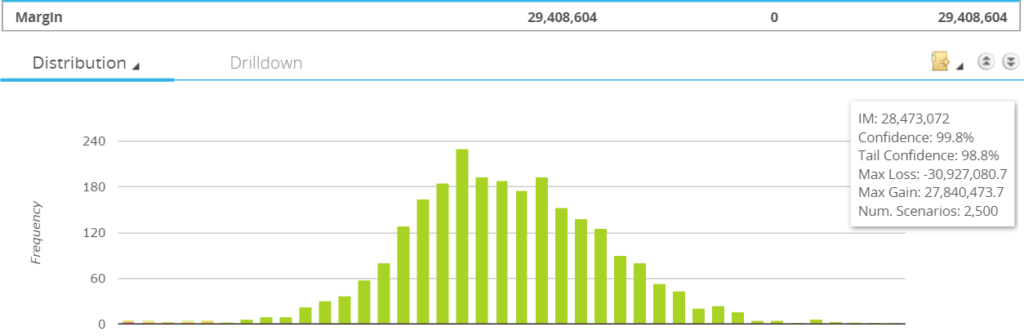
Using CHARM, we can quickly run this portfolio at both LCH and CME. For LCH, we see the following Initial Margin analysis;
Showing;
- An Initial Margin of $29.4m
- To recap, this is based on 2,500 scenarios and taking the average of the worst six losses
- The green histogram shows the distribution of outcomes from these 2,500 scenarios
- Computationally, this is a very different approach to ISDA SIMM.
What about CME? Running the same portfolio shows an IM requirement of $23.8m. Slightly lower than at LCH, in line with Amir’s review of the two IM models that we published way back in 2014.
Remember that we have calculated an uncleared Initial Margin Requirement of $36.13m for this same portfolio. We can therefore say that:
- Uncleared IM is 52% higher than at CME.
- Uncleared IM is 23% higher than at LCH.
- This assumes that the portfolio is traded with a single counterparty in Uncleared space. This is unlikely, and hence the lack of netting between counterparties means that the Uncleared IM for this portfolio will actually be much higher.
- The difference between Uncleared IM and LCH IM is broadly equal to the difference between IM at CME and IM at LCH.
Systematically Adding Risk
Playing around with ballpark numbers for sample portfolios is a good place to start. But to understand the numbers (and to help verify our computations), we need to do some systematic analysis too.
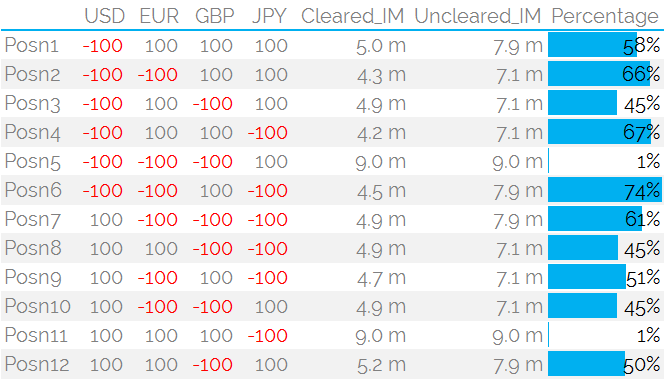
Let’s start with a portfolio of $100k DV01 in USD Rates and compare different combinations of EUR, JPY & GBP $100k positions. We’ll compare Uncleared IM with Cleared IM at LCH.
Showing;
- 12 different combinations of Pay/Receive for $100k DV01 of 10 year risk in each of USD, EUR, GBP and JPY.
- ISDA SIMM is symmetrical, LCH tends to be fairly symmetrical too.
- ISDA SIMM is always higher than LCH…
- …but in the case of large directional positions across EUR, GBP and USD rates (i.e. normal volatility currencies) the Margin numbers between Cleared and Uncleared converge….
- ….whilst others see margins 74% higher if left Uncleared.
- Remember that ISDA SIMM aims for a 99% confidence interval over a 10-day observation period. The model is not calibrated against CCP margins, but rather against a 1y stress period and a 3 year “normal” period.
- Again, it is worth starting that due to the lack of netting between counterparties, a real portfolio with multiple counterparties will always have a higher IM than at a CCP.
Some of the results above are a little surprising to me – such as positions 2,3,4 etc all having identical IM under ISDA SIMM, despite JPY having a different risk weighting. I also expected positions 5 and 11 to be much higher under ISDA SIMM.
In Summary
- It is straightforward to calculate ISDA SIMM IM for multi-currency portfolios.
- The resulting Uncleared IM requirements are higher than if the portfolio were cleared at a CCP.
- But the differences vary according to the risk profile….
- …in the case of some portfolios, the IM requirement can actually be very close between Cleared and Uncleared portfolios.
- But Uncleared IM can also end up being 74% higher.
- It is therefore vital to model real portfolios and understand the drivers of IM under different conditions.
- UPDATE: We now offer free 14-day trials for our SIMM for Excel product.