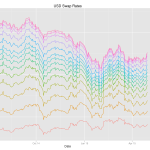
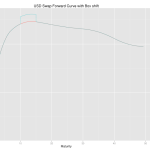
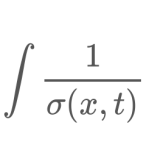Principal Component Analysis of the Swap Curve: An Introduction
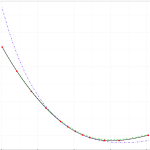
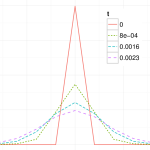
Principal Component Analysis (PCA) is a well-known statistical technique from multivariate analysis used in managing and explaining interest rate risk. Before applying the technique it can be useful to first inspect the swap curve over a period time and make qualitative observations. By inspection of the swap curve paths above we can see that; 1. […]
Swap Equivalents via Waves
In a recent paper, “Calculating Delta Risks and Hedges via Waves (2015)“, Hagan deals with an old practical problem–determining risk and hedges on an interest rate book. In older systems a delta hedge report is often implemented by perturbing quotes used to construct the yield curves, restripping the curves and then revaluing the book. As […]
Computus: Algorithms to compute Easter
With Easter arriving this weekend, I thought it might be interesting to mention something on the algorithms used to compute Easter. As we know, Easter is a not a fixed date each year, it is determined by the rule Easter is the first Sunday after the first full moon occurring on or after the vernal […]
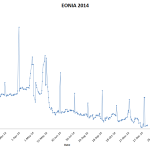
Year End Turn Rates
The year-end turn-rate (or the turn-of-the-year rate) is the interest rate for the period between the last business day of the year until the first good business day in the next year. For example, in the US the 2014 turn rate is the interest rate for the period between 31-Dec-2014 until 2-Jan-2015. The rate can […]
Lamperti Transform
Let \(X_t\) be an Ito process given by $$dX_t=f(X_t,t)dt+\sigma(X_t,t)dw_t$$ The Lamperti transformation is, $$Z_t=\phi(X_t,t)=\int\frac{1}{\sigma(x,t)}dx$$ and has a unit diffusion; that is, \(dZ_t=(…)dt + dw_t\). This transformation is fairly well used in finance, and particularly useful with separable volatility functions both in analytic and numerical contexts. However I am not sure the name is well known […]
SABR Calibration: A simple, explicit initial guess
The SABR model is widely used, particularly in the interest rate world, to help manage the volatility smile. Depending on 4 parameters, \(\alpha\), \(\beta\), \(\rho\) and \(\nu\), often \(\beta\) is considered a fixed constant whilst the other 3 parameters are calibrated to liquid market prices. There tends to be two types of calibration algorithms; local […]
Arbitrage-Free SABR: Finite Difference Techniques
In January a new approach to the SABR model was published in Wilmott magazine, by Hagan et al., the original authors of the well-known SABR model. They review some of the weaknesses of the model, and concentrate on the problem of negative probabilities induced by the original approximation formula, especially at low strikes. To solve […]
Fed Fund Swap Nuances
A few people have recently asked me about the details of USD Fed Fund Swaps. I collected some of my answers together in this post for convenience. Fed Fund Swap and OIS Swap differences Fed Fund Swaps and OIS swap are easily confused at first glance, both are swaps involving the Federal Funds rate, both […]
Valuation of Massive OTC Portfolios: From Milli-Seconds to Micro-seconds
In the not to distant past I can recall seeing several risk systems valuing vanilla interest swaps with individual trade valuations taking around a few milliseconds. Whilst quants might rightly be alarmed that it would take so long, when one adds in overheads which can easily occur in the integration of a pricing library with […]
Computing ATM implied volatility analytically
I recently had to compute ATM implied bpvol (or normal volatility) as well as Black volatility from an ATM option premium. Immediately, I looked for a library function which, more often than not, are written for the general case and make use of a solving routine. To my later irritation, I had completely forgotten that […]