- Only a small portion of the NDF market is cleared
- We present theoretical exposures within bilateral and multilateral dealer networks to illustrate the reduction in Initial Margin that multilateral netting offers
- We can see that the motivation to clear varies with a dealer’s position
- And as positions change over time, more clearing leads to greater reductions in IM
After my post last week about NDF trading, I was intrigued enough about the lack of Clearing to start running some numbers. Below is a framework that looks at the possible multilateral netting benefits for Initial Margin.
What is multilateral netting?
In terms of OTC Derivatives, multilateral netting can be considered as:
A process that sums up all offsetting positions to create one overall position
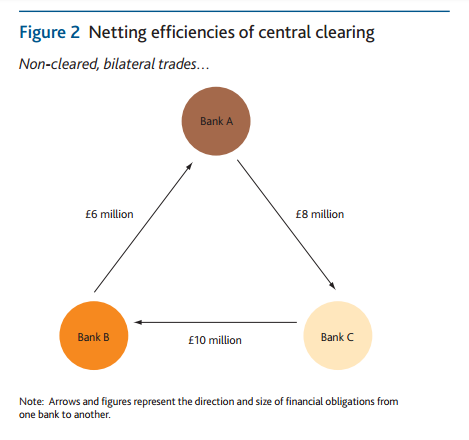
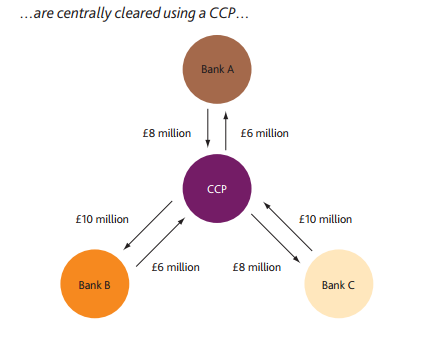
In general, this is achieved by the insertion of a Central Counterparty between the buyer and seller of any given contract. In the case of Interest Rate Swaps, this may take the form of novation to e.g. LCH SwapClear, who will then also guarantee the payments for the life of the trade – even in the event of a default. The Bank of England have a good paper that looks at this, and a nice diagram that illustrates the concept better than I can put it into words (click to enlarge).
All well and good. So why bring this up in relation to my blog on NDFs?
Bilateral Margin
As we touched upon last week, Margin for Uncleared Derivatives (let’s introduce UMR, Uncleared Margin Rules, for that mouthful) is about to come into play for the largest counterparties in September 2016. This will mean that NDFs are subject to bilateral margining.
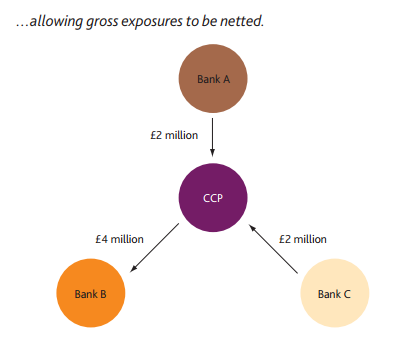
Multilateral netting benefits within clearing reduce gross bilateral counterparty exposures down to a single net exposure to the CCP. This not only has the benefit of reducing credit exposures, but will therefore also reduce the amount of Initial Margin that has to be held (compared to retaining the same exposures in the bilateral world).
This might not be immediately obvious, so I’ve run some numbers to illustrate this.
Dealer Network
For simplicity, let’s consider a 6 dealer network – as dealers will be the first to be captured by the UMRs. We’ll assign some random exposures between them all:

Because the exposures are random, we see a wide range of IM. Therefore, not every dealer has the same motivation to start Clearing their trades as every other dealer.
In the random example above, we see that Dealer 2 has a long position (positive exposure) with every other dealer. Let’s look at how their Margin changes as the percentage of the market that is being cleared changes:
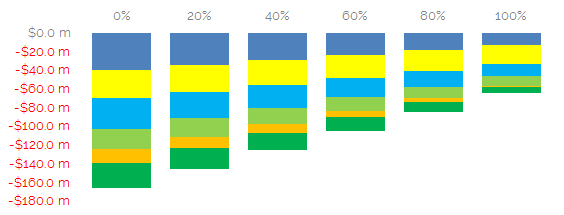
- Dealer two is in yellow.
- When there is no clearing, the IM is nearly $30m in this example (I have used random, but symmetrical, PnL vectors).
- When 40% of the market is cleared, this IM number reduces to $26.3m.
- It reduces in a linear manner until 100% of the market is cleared and Dealer 2 has an IM of $21m. In our model, this is the minimum amount of IM that their net risk will allow.
- Compare this to any of the other Dealers. Dealer 1 (in blue) reduces their IM from $40m to $13m once the whole market is cleared. Dealer 5 reduces IM from $14.5m to just $1m.
- The reductions are not only a function of the net risk, but also how this risk is spread amongst counterparties in bilateral space. For example, Dealers 1,3 and 4 have similar net risk amounts. And yet their reduction of IM with clearing varies from 32% up to 46%.
Plausible Scenarios
The above example is just one set of random numbers. We need to apply this to the real World. Here are some thoughts on doing that:
- For long-dated derivatives positions, such as an Interest Rate Swaps portfolio, it is fairly likely that dealers will have built up structural positions that will exist for a considerable period of time. This is down to biases within their franchises, and the fact that the market built up momentum long before Clearing did.
- I wonder if the same holds true for short-dated derivatives portfolios such as NDFs? There are bound to be some kind of structural biases from one bank to another (e.g. some banks will be stronger in offshore markets, others will also have an onshore presence). But because the positions are more likely to roll-off in a short time-period, the portfolios should refresh at a far quicker rate than for Interest Rate Swaps.
- I’d like to suggest, therefore, that for these shorter-dated products, dealers are unlikely to know what their structural bias will be from one quarter to the next.
- It is therefore appropriate to model their positions randomly, to see what the market as a whole can expect if Clearing does take off.
Results
Given all of that, I ran 1,000 random networks to see how IM changes per dealer from the bilateral space to the cleared space. I modelled different levels of clearing from 0% to 100% to check that there is a linear relationship between the reduction of IM (on average) and the amount of clearing. The histogram of results is shown below:
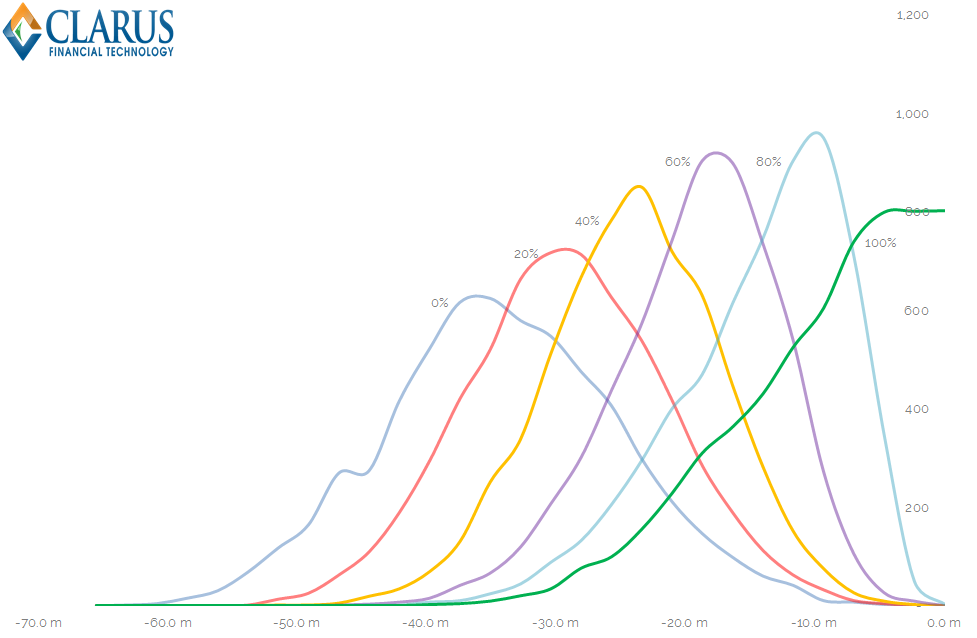
Showing;
- Total Margin along the x-axis – the sum of bilateral margin plus cleared margin per dealer. (I have multiplied cleared margin by the square root of 10 over 5 to take into account the different holding periods within the return calculations).
- Along the y-axis are the number of observations (out of a total of 6,000 – one thousand per dealer, six dealers) within an IM range.
- Each data series represents a different portion of the total volume being cleared – from 0% up to 100%.
- We can see that, on average, absent any clearing whatsoever, dealers can expect to have an IM level of nearly $40m using the random variables in this example.
- This decreases (i.e. the peak of the distribution gradually moves toward zero), as the amount of clearing within the market increases.
- If Clearing accounted for 80% of volumes within the market, dealers could expect an IM level of under $10m. Importantly, less than 3% of observations have IM levels greater than $30m when 80% of the market is cleared.
Some Caveats
Remember that all of the numbers presented here are random and not based on actual positions or IM numbers. We’d have to look at an NDF clearing model to put in accurate IM numbers for some given notional amounts. But the theory holds.
I thought this would be a rock-solid way to present “Clearing good, bilateral bad”, but after a little bit of research into the academic material on this subject, it appears there is a degree of disagreement as to whether “Clearing good, bilateral bad” holds under ALL conditions.
Specifically, Duffie and Zhu (2011) present a model that looks at the impact of introducing a new CCP to a multi-asset cleared world. They suggest that netting can be decreased if multiple CCPs are competing for market-share within the same asset-class, and further that multiple CCPs clearing multiple derivative classes increases counterparty exposures. However, Cont and Kokholm (2012) refute this claim when they introduce different levels of “riskyness” between the derivative asset classes.
It’s not the work of a blog to review and critique those pieces of work – but both papers make very accessible arguments and are worth 30 minutes of your time.
In Summary
- We are intrigued why a large portion of the FX NDF market trades on SEF, but does not Clear.
- We therefore compare theoretical IM levels in a dealer-to-dealer network under Bilateral and Cleared margin models.
- We find that, on average, a network of 6 dealers will see a reduction in IM levels of 75% once 80% of volumes are cleared.
- That seems a compelling argument for the market to reconsider Clearing before the UMRs are in force later this year.