- Various risk charges must be calculated under the Standardised Approach of the FRTB.
- These risk charges are split into Delta, Vega and Curvature.
- Curvature Risk Charge is complicated to calculate as we must record MTM changes to large input shocks.
- We explain the calculations involved.
- For Rates products, the Curvature Risk Charge is not split by tenor or index, therefore yields a single charge per currency.
Fundamental Review of the Trading Book
I am going to dig deep into the calculations required to explain the FRTB Standardised Approach for option products. This second blog will tackle the Curvature Risk Charge. Whilst the commentary concentrates on Rates products, the methodology is extensible into all other asset classes.
Our reference document throughout is the BCBS January 2016 publication “Minimum Capital Requirements for Market Risk.” With a working (and recently updated) ISDA SIMM IM model in Excel, the similarities of the calculations are striking for the most part. Whilst we covered Curvature Risk in our ISDA SIMM Swaptions blog, the FRTB approach is distinctly different.
1. Risk Inputs & Weights
Curvature Risk is a tricky one to pin-down. The methodology asks us to provide a large shock to the price of the underlying and to measure the valuation impact. Only trades with optionality are to be included in this exercise.
It is akin to “stress-testing” an options portfolio, offering a pragmatic way to incorporate a catch-all of non-linear risks.
Curvature covers second-order risks arising from option positions exposed to very large moves of the underlying. It will therefore cover gamma positions as well as smile risk for swaptions (see here), but exclude convexity for linear products.
Exotic trades (such as digitals and barriers) will be the bulk of trades making up the Residual Risk Add-On, which Amir has looked at previously. This add-on is calculated based upon notional and is in addition to the Delta, Vega and Curvature Risk Charges that an instrument may incur.
To calculate the Curvature Risk Charge, we must answer the following questions:
- How do we define a “large move in the underlying”?
- How do we avoid double-counting the delta risk charge?
These issues are covered by the complicated-looking formula:
\( \tag {1} \large CVR_{k} =-Min {\sum\limits_{i}[V_{i}(x_{k}^{+/-RW})-V_{i}(x_{k})-s_{ik}.RW_{k}]}\)Which in simple terms says:
- Take the value of your instrument when Rates are equal to level \( x \) (i.e. at market).
- Move all Rates up by the Risk Weight, \(RW\).
- Calculate the value of your instrument at these new rates.
- Remove the impact of the linear Delta Risk by subtracting the delta risk charge (delta sensitivity, \( s_{ik}\) multiplied by the Risk Weight, \( RW_{k}\)).
- Repeat for a move down in Rates by the same Risk Weight.
- Take the minimum (likely most negative) value of the two and multiply by minus 1. This is your Curvature Risk Charge for that instrument.
This leaves one outstanding question. How much should we move Rates by? We refer to the Risk Weights used in our Delta Risk Charge calculation:
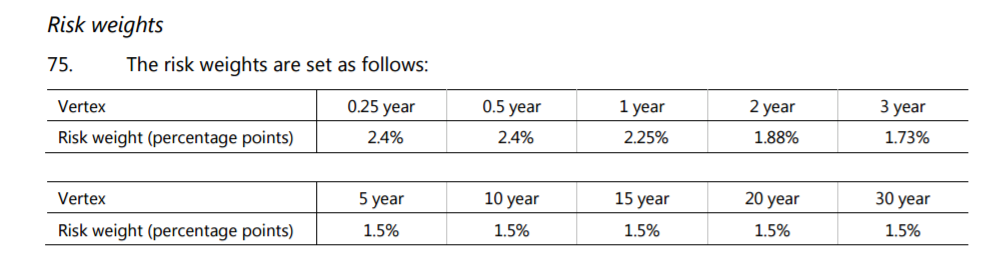
According to the BCBS calibration, we simply take the highest value from the above grid and apply it to every single maturity. So in effect, we shock the whole curve by 2.4%. It therefore follows that, if the instrument is at-market currently (i.e. has a zero MTM) what we are actually doing is:
Value of instrument “i” after a 2.4% move in Rates – (DV01 of “i” x 240)
As we saw in our Delta Risk Charge calculations, the Risk Weights to be applied are currency dependent:
Accordingly, for those 7 currencies (plus domestic), the shock that we apply will actually be 1.697%.
An Interpretative Note
At this juncture, I need to point you in the direction of paragraph 59(e) on page 22. For Rates options, this clearly states (emphasis mine):
The GIRR risk factors are defined along only one dimension: the constructed risk-free yield curve per currency: For example, the Eonia, Euribor 3M and Euribor 6M curves must be shifted at the same time.
Therefore, despite the documentation providing a lot of focus on aggregating across different risk factors (“k”, which equate to different index curves in the Delta Risk Charge for Rates products), we actually bump each index curve at the same time. This therefore yields a single Curvature Risk Charge (in Rates) per currency.
This also means that we take the net DV01 across all of the index curves per currency to subtract the delta risk charge.
2. Correlations (within currency aggregation)
As with all of the FRTB and ISDA SIMM calcs, the devil is in the aggregation formulae for the individual sensitivities to each risk factor, k. Curvature Risk is no different.
For a pure Rates option, this aggregation step will not apply, as all index curves are bumped simultaneously. However, it will apply to e.g. CDS options referencing a basket of underlying names.
We aggregate across our risk factors using a familiar-looking co-variance equation:
\( \tag {2} \large K_{b} = \sqrt{max(0,\sum\limits_{k}({CVR_{k},0)^2+{\sum\limits_{k}}{\sum\limits_{k≠l}ρ_{kl}CVR_{k}CVR_{l}ψ(CVR_{k},CVR_{l}))}}}\)Where;
\(CVR\) is the Curvature Risk Charge to each risk factor.
\(ρ_{kl}\) is the correlation to use between risk factors. This effectively disappears in Rates as all indices are bumped at the same time. For other asset classes, remember to use the square of the \(ρ_{kl}\) values used in the Delta Risk Charge calculations.
\(ψ(CVR_{k},CVR_{l})\) is zero if both \(CVR_{k}\) and \(CVR_{l}\) are negative. Otherwise, it is 1. To my mind, this means that we don’t recognise additional benefits from two long gamma positions within the same bucket/currency.
3. Multi Currency Curvature Risk Charge (across currency aggregation)
More pertinently for Rates, we must combine the individual currency Curvature Risk Charges into a single Curvature Risk Charge for the risk class of Rates. This is achieved using another familiar formula:
\( \tag {3} \large Curvature Risk Charge = \sqrt{\sum\limits_{k}{K_{b}^2+{\sum\limits_{b}}{\sum\limits_{c≠b}γ_{bc}S_{b}S_{c}ψ(S_{b},S_{c})}}}\)If you’ve got this far, that is all pretty self-explanatory. It is just worth bearing in mind our notes from ISDA SIMM and ISDA SIMM Swaptions that:
\( {S_{b}}\) is either the sum of all of the “Kb” terms or the value of \( K_{b} \) for currency b. We first take the smaller of the sum of the Kb‘s and then the larger of this and “\( K_{b} \)” for currency b.
For the purposes of all Curvature Risk calculations, we square the previously calibrated correlations that we used to calculate the Delta Risk Charge. Therefore, \( γ_{bc} \) takes the value of 50%^2 = 25%.
Finally, remember to run the high, medium and low correlation scenarios as we explained at the bottom of this blog.
In Summary
- The Curvature Risk Charge is applicable only to options products.
- For Swaptions in particular, the FRTB calculations diverge significantly from those used in ISDA SIMM.
- The implementation for FRTB has more to do with how the shocks are applied, rather than introducing another exercise in building co-variance matrices/designing Excel spreadsheets.
- For Rates products, it is key to note that all index curves must be bumped simultaneously.
- Curvature Risk Charge is therefore akin to stress-testing an options portfolio.
- Broadly speaking, the Curvature Risk Charge incorporates second-order risks arising from large moves in the price of the underlying.


Thanks, Chris. If we bump all curves up together to calculate one CVR per currency, how to calculate RWk*Sik in 53 (b)? My understanding is we sum all delta for each trade but how to handle Xccy Basis Curve? sum(all delta for each trade) + XccyBasisParallelDelta. It looks like you treat weighted all delta sum as the delta risk charge. Can you clarify this part?
Thanks
Many thanks for the question. It’s one I had trouble interpreting from the documentation. At first, I thought it would make sense to bump each curve independently, exactly because we have to remove the delta effect. However, paragraph 59e clearly states that we bump at the same time. I think what you suggest makes sense – just aggregate all deltas together for that currency across all indices and multiply by 240bp. It would make sense to treat the XCCY curve as your discount curve, so just another delta to add into the mix.
Thanks, Chris. When we apply weight on delta for Curvature, do we apply 240 bp or 240/SQRT(2) if the note 24 in page 29 is satisfied? My understanding this could be consistent with vertex weight for GIRR Delta. If it is major currency then 240/SQRT(2). Otherwise we should apply 240 bps.
Cheers
Juki
Agreed, 169.7 for the majors!