Following on from my articles, Fundamental Review of the Trading Book and Internal Models or Standardised Approach, I wanted to take a look at a specific component of the Market Risk Capital, namely the Default Risk Charge as required under the Standardised Approach.
Background
In January 2016, the Basel Committee on Banking Supervision (BCBS) published its Standards for Minimum Capital Requirements for Market Risk; also known as the Fundamental Review of the Trading Book (FRTB). These new standards replace parts of the Basel 2.5 reforms, which were introduced in 2009 to address the material undercapitalisation of trading book exposures during the 2007-08 financial crisis. (Document is here).
Standardised Approach (SA)
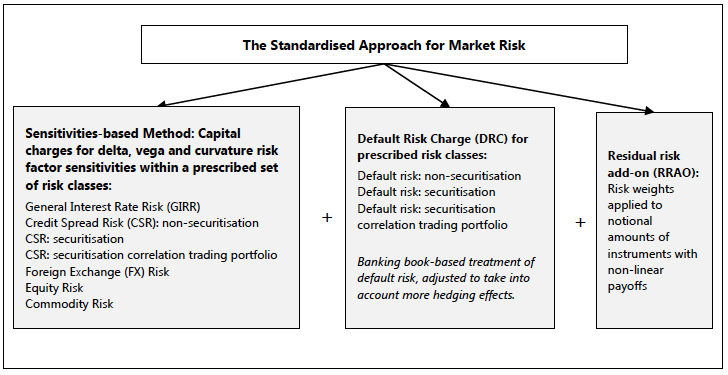
The overview chart from the BCBS document:
In my article, Uncleared Margin, ISDA SIMM and FRTB SA, I looked at the fact that the ISDA SIMM methodology is based on and very similar to the Sensitivities-based Method as detailed in the left hand box above, while the Default Risk Charge is not applicable to SIMM and risk margin.
Default Risk Charge
The Default Risk Charge is intended to capture the Jump-to-Default (JTD) risk of an instrument i.e. the loss that would be suffered by the holder if the issuer of the bond or equity were to default. It is computed for each instrument separately and is a function of the face amount (or notional) and market value of the instrument and the Loss Given Default (LGD). The change in market value due to credit quality is captured by the Sensitivities Delta charge for Credit Spread Risk factors.
The Default Risk Charge is distinct from a Counterparty to a trade defaulting, which is capitalised under Credit Risk and not Market Risk
There are three calculation steps:
- Gross JTD risk positions (Gross JTD)
- Net JTD risk positions (Net JTD)
- Default risk charge (DRC) for non-securitisations
We will look at these in detail by extracting the key sections from the BCBS document, keeping their paragraph numbers for ease of reference.
(The DRC for securitisation is similar but different enough that I will not have time to cover in this article).
1. Gross JTD
139. As a first step, the gross JTD risk is computed, exposure by exposure. For instance, if a bank is long a bond on Apple, and short another bond on Apple, it must compute two JTD exposures.
140. The determination of the long/short direction of positions must be on the basis of long or short with respect to the underlying credit exposure. (Long exposure being when the default of the underlying obligor results in a loss).
142. The gross JTD is a function of the LGD, notional amount (or face value) and the cumulative P&L already realised on the position:
- JTD (long) = max (LGD x notional + P&L, 0)
- JTD (short) = min (LGD x notional + P&L, 0)
where notional is the bond-equivalent notional (or face value) of the position and P&L is the cumulative mark-to-market loss (or gain) already taken on the exposure. In more detail, P&L = market value – notional.
143. In the equations, the notional of an instrument that gives rise to a long (short) exposure is recorded as a positive (negative) value, while the P&L loss (gain) is recorded as a negative (positive) value.
144. Equity instruments and non-senior debt instruments are assigned an LGD of 100%. Senior debt instruments are assigned an LGD of 75%. Covered bonds are assigned an LGD of 25%.
145. The starting point is the notional amount and mark-to-market loss already realised on a credit position. The notional amount is used to determine the loss of principal at default, and the mark-to-market loss is used to determine the net loss so as to not double-count the mark-to-market loss already recorded in the market value of the position.
146. To account for defaults within the one year capital horizon, the JTD for all exposures of maturity less than one year and their hedges are scaled by a fraction of a year. No scaling is applied to the JTD for exposures of one year or greater. For example, the JTD for a position with a six month maturity would be weighted by one-half, while the JTD for a position with a one year maturity would have no scaling applied to the JTD.
2. Net JTD
150. The gross JTD amounts of long and short exposures to the same obligor may be offset where the short exposure has the same or lower seniority relative to the long exposure. For example, a short exposure in an equity may offset a long exposure in a bond, but a short exposure in a bond cannot offset a long exposure in the equity.
151. In the case of long and short offsetting exposures where both have a maturity under one year, the scaling can be applied to both the long and short exposures. Finally, the offsetting may result in net long JTD amounts and net short JTD amounts (which are aggregated separately as described below).
3. DRC
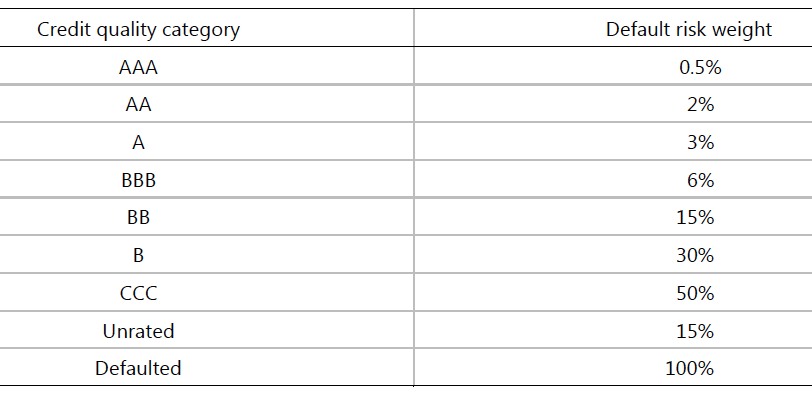
152. Default risk weights are assigned to net JTD by credit quality categories (i.e rating bands), irrespective of the type of counterparty, as in the following table:
153. The weighted net JTD are then allocated to buckets. The three buckets for this purpose are corporates, sovereigns, and local governments/municipalities.
154. In order to recognise hedging relationship between long and short positions within a bucket, a hedge benefit ratio is computed.
155. The overall capital charge for each bucket is to be calculated as the combination of the sum of the risk-weighted long net JTD, where the summation is across the credit quality categories , the WtS, and the sum of the risk-weighted short net JTD, where the summation is across the credit quality categories:
Where DRC stands for “default risk charge”, and i refers to an instrument belonging to bucket b.
156. No hedging is recognised between different buckets. Therefore, the total capital charge for default risk non-securitisations must be calculated as a simple sum of the bucket-level capital charges. For example, no hedging or diversification is recognised across corporate and sovereign debt, and the total capital charge is the sum of the corporate capital charge and the sovereign capital charge.
Thats it.
While the steps might seem verbose, they are as brief as I could extract from the BCBS document and still cover the key elements.
Lets look at some examples of these in practice.
Example 1 – Bond and CDS
Our position is:
- $100m in a Corporate Bond with Credit Quality of A, and
- $50m Credit Default Swap buy protection on the same Issuer
For simplicity we will assume zero PL on each exposure and LGD for senior debt is 75%.
- Gross JTD, we calculate, JTD (long) = $75m and JTD (short) = $50m
- Net JTD, we calculate, Net JTD (long) = $25m
- DRC, using the 3% risk weight for Single A Credits, gives DRC = $750,000.
Example 2 – Equity
Our position is:
- $40m in a Equity, where the Issuer is a BB Credit Quality
And for simplicity we will assume zero PL on each exposure and LGD for Equity is 100%.
- Gross JTD, we calculate, JTD (long) = $40m.
However from the BCBS document, we also have the following, “147. Cash equity positions (ie stocks) are assigned to a maturity of either more than one year, or 3 months, at firms’ discretion.” So lets assume 3 months or 25% for the maturity weighting (because we can):
- Gross JTD, we calculate, JTD (long) = $10m
- Net JTD, we calculate, Net JTD (long) = $10m
- DRC, using the 15% risk weight for BB Credits, gives DRC = $1.5m.
Example 3 – Credit Default Swap
Our position is:
- $40m in a CDS, where we have sold protection on a Corporate with BBB Credit Quality
- Gross JTD, we calculate, JTD (long) = $30m (using 75% LGD).
- Net JTD, we calculate, Net JTD (long) = $30m
- DRC, using the 6% risk weight for BBB Credits, gives DRC = $1.8m.
Example 4 – Bond and Equity
Our position is:
- $25m short a Corporate Bond with B Credit Quality
- $20m long an Equity (same Issuer)
- Gross JTD, we calculate:
- JTD (long) = $20m (using 100% LGD), and
- JTD (short) = $18.75m (using 75% LGD)
- Net JTD, we calculate the same net JTD long and JTD short as “a short exposure in a bond cannot offset a long exposure in the equity”.
- DRC, using the 30% risk weight for a B Credits, is more involved and using:
The first term is $6m, while WtS = 0.52, making the second term $5.625m
Assuming my assumptions are correct, DRC = $3.1m and so much higher than the simple net of $375k, showing that the effect of he hedging benefit ratio.
(I do have a concern that in this case I cannot net here at all and DRC = $6m, if you know, please email me).
Example 5 – Putting it all together
Now lets assume we hold all the above positions but each in a different Corporate Issuer.
- Gross JTD are as above because these are Issuer (obligor) specific results.
- Net JTD are also as above
- Step 3 DRC is where it all happens.
The first term in our DRC equation is a sum of all the net JTD (long) and their Risk Weights :
- $750k + $1.5m + $1.8m + $6m = $10.05m
WtS is 85m/(85m+18.75m) = 0.82, (using the long and short exposures) making the second term:
- 0.82 * abs(-5.625m) = $4.61m
DRC is then $10.05m – $4.61m = $5.44m.
Does not sound too big, but of course the actual DRC for Trading Desk would be far higher.
Thats it for the examples.
(Any mistakes are all mine, apologies in advance).
Final Thoughts
Default Risk Charge is required for Market Risk Capital.
The Standardised Approach for DRC is straightforward, as shown above.
It’s assumptions and use of gross measures will lead to a conservative measure.
One certainly a lot higher than an Internal Models approach for DRC.
However Securitisation exposures in the trading book cannot use Internal Models for DRC.

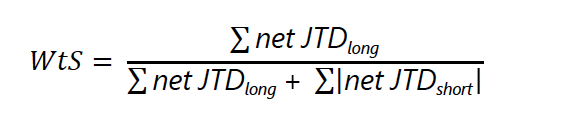
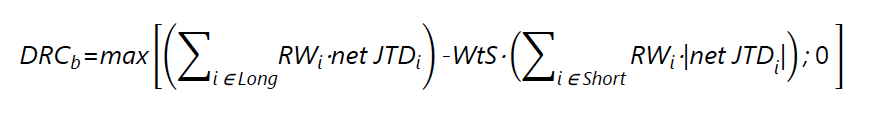
Very good summary with crystal clear!