Mechanics and Definitions of SA-CCR (Part 3)

Please note: this is Part Three of a series. Part one of the story for SACCR provided critical background regarding key terms and concepts. Part Two covered the Maturity Factor and how different CSAs and/or treatments of derivatives impact SACCR calculations.

We now need to look at how the SACCR calculations unfold in terms of netting.

Revisiting CEM (briefly)

SACCR is meant to introduce a risk-sensitive measure of exposures. The Current Exposure Methodology was based on Gross Notional alone. There was no offset for the simultaneous buy and sell of the same risk factor with the same counterparty – the exposure would “gross up” to twice the size, even if it took the relationship risk neutral. This is why compression (tearing up risk neutral packages of trades) became such an obsession for a newly leverage ratio (SLR)-constrained portion of the market.

When we used CEM, we never had to concern ourselves with netting. Instead we just took the gross amount of notional at a point in time across all trades within an asset class. For example, in FX:

Potential Future Exposure under CEM at a trade level = Gross Notional * Add-On

The Add-On did vary by maturity:

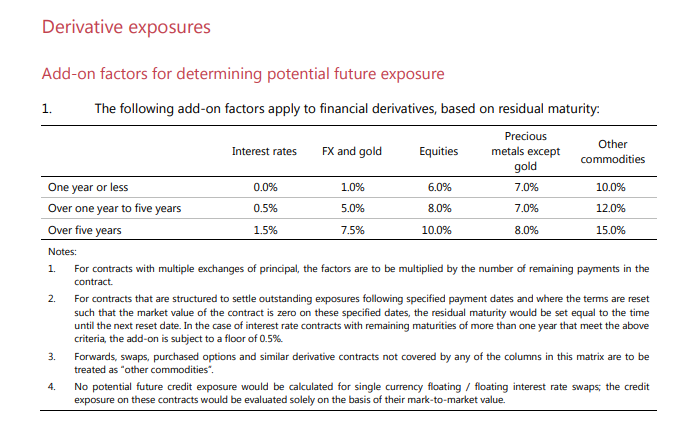
But the CEM calculation was essentially a look-up function. Notional * Add-On = PFE

We did this for all currencies – it didn’t matter if I was looking at a EURUSD, or a JPYUSD or a EURJPY trade. I just calculated the add-on value (Notional * Add-on) per line item and did a gross sum to get my total PFEs. Very simple.

In the case of FX, with so much of the gross notional sub 1 year, most of the time I was calculating 1% of gross notional as my add-on value for real portfolios.

Netting Sets & Hedging Sets

SACCR is different. I must consider both Netting Sets and Hedging Sets. Let’s consider a Netting Set:

52.7 A netting contract with the counterparty or other agreement which creates a single legal obligation, covering all included transactions, such that the bank would have either a claim to receive or obligation to pay only the net sum of the positive and negative mark-to-market values of included individual transactions in the event a counterparty fails to perform due to any of the following: default, bankruptcy, liquidation or similar circumstances.

BCBS CRE 52

If you think of a complex interdealer bilateral relationship, they are normally governed by an ISDA Master Agreement. As part of this, a Credit Support Annex (CSA) governs what collateral needs to be posted each day versus the variation in market values of the portfolio. There are highly likely to be FX swaps, Swaptions, FX Options, Equity total return swaps and some type of commodity trades covered by this CSA at a minimum. Despite the complexity, there will typically be a single transfer of collateral each day to cover the whole portfolio.

As we saw in Part Two of this series, the SACCR output is highly sensitive to the specifics of this netting agreement and accompanying CSA. How many trades are covered, are some “hard to value” etc. However, we also need to know what the exposures are within the netting set.

This is where Hedging Sets come in to play. From BCBS:

The trades within each asset class are separated into supervisory specified hedging sets. The purpose of the hedging sets is to group together trades within the netting set where long and short positions should be permitted to offset each other in the calculation of potential future exposure.

BCBS CRE52.30 (3)

Calculating Adjusted Notional Facing a Counterparty

It’s pretty straightforward really. The process goes:

1. Do I have an ISDA with the counterparty (or some other legally enforceable netting agreement).
2. If Yes, then I break the trades down into Hedging Sets. FX trades all placed into a single “bucket” but split by currency pair, Rates trades are placed in 3 offsettable “buckets” within each currency etc.
3. The Hedging Sets benefit from a net notional versus the supervisory factor. If I am looking at all EURUSD trades facing a counterparty, I take the net notional facing the counterparty. I also take the net notional of GBPUSD trades. I then take the absolute value of each of the EURUSD and GBPUSD net notional amounts to calculate an “adjusted notional” facing the counterparty.
4. If there is no netting agreement, all trade level calculations are done gross. There is no offset or benefit from netting.

---

Adjusted Notional for Rates

As we looked at previously in “SA-CCR: Explaining the Calculations“;

Trade Level Adjusted Notional

[Once the dates on a trade] are adequately described, we can move forward with some calculations regarding the risk of a trade. First, we must consider adjusting the trade notional according to the following equation:

\( \tag {1} d_{i}  =  TradeNotional * \frac{exp(-5\% * S_{i}) – exp(-5\% * E_{i})}{5\%}\)

For interest rate swaps that have already started, we are simply taking “e” to the power of a negative multiplier of 5%. Hence the effective multiplier to the trade notional increases as maturity increases.

That calculation gives us a “delta-like” value at a trade level. And then, in terms of netting for Rates;

Step Six – Aggregate Across Maturities

We now aggregate these values of \( D_{i}\) at a currency level. Each trade is grouped into either a sub-one year, 1-5 year or 5 year plus maturity bucket. The values of \( D_{i}\) are summed together within each maturity bucket, and then aggregated across maturities according to the following:

\(\tag {5} EffectiveNotional_{CCY} = \sqrt {[D_{1}^2 +D_{2}^2+D_{3}^2 + 1.4*D_{1}*D_{2} + 1.4*D_{2}*D_{3} + 0.6*D_{1}*D_{3}]}\)

Our eagle-eyed readers will no-doubt recognise the similarity of this equation with those we implement for ISDA SIMM and FRTB…

---

Add-On for FX

Armed with the above knowledge, the calculations for SACCR are frighteningly straightforward:

1. Identify netting agreement with counterparty.
2. Identify different hedging sets within portfolio.
3. Calculate Adjusted Notional per hedging set. For FX products, this is as simple as calculating the net notional per currency pair.
4. Multiply it all together, along with the Maturity Factor and “Supervisory Factor” per asset class.

From last week’s blog, we know all about the Maturity Factors and how they can vary:

MPOR	Maturity Factor	Comment
40	0.60	Disputed CSAs
20	0.42	Hard to value trades; 5,000+ netting sets
10	0.30	CCPs, “clean” CSAs
STM (Settled to Market)	0.20	Settled to Market

So let’s finish up by introducing the Supervisory Factors.

“Risk Weights” per Asset Class

In a table that looks, at first glance, somewhat similar to the old CEM Add-On table, the BCBS publish the effective risk weightings per asset class:

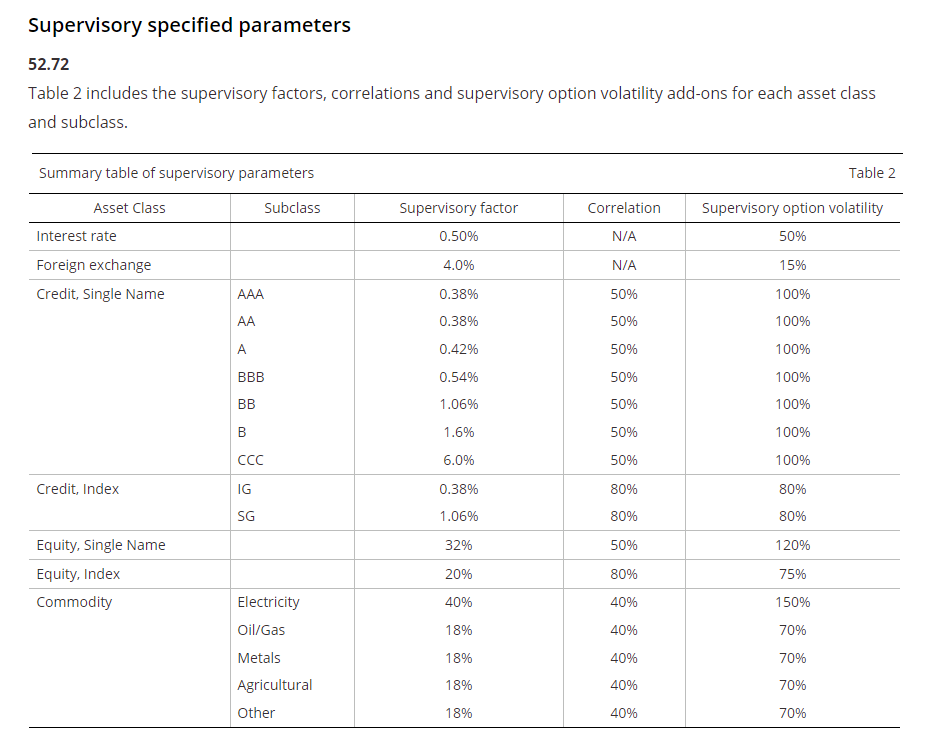
Any Adjusted Notional or Effective Notional that we calculate in the interim steps for SACCR calculations, we multiply by the asset class-appropriate Supervisory Factor above. For example, FX has a risk weight of 4%, Rates is just 0.5%.

Alpha

As we stated in SACCR Part One;

Alpha. This is a regulatory defined term of 1.4. What does this mean? It inflates all of the calculations under SACCR by 40%, therefore any non-zero element of a SACCR calculation effectively attracts a 40% “add-on” that was not there under CEM.

Remember this for the next step….

Exposure at Default for FX

The final step reminds us again that all we do for SACCR is multiply the terms together. It all sounds so trivial when summarising in a blog post:

Exposure at Default for FX = Net Notional * Maturity Factor * Supervisory Factor * Alpha (1.4)

Let’s show a worked example to make this really, really obvious:

Net notional EURUSD	$100m
Maturity Factor CSA with <5,000 trades, clean CSA	0.30
Supervisory Factor	4%
Alpha	1.4
Calculation	100 * 0.30 * 4% * 1.4
Exposure at Default (EAD)	$1.68m

After 1,200 words, I end up with a very simple proxy: An FX trade consumes ~1.68% in regulatory capital (assuming the leverage ratio is the capital constraint). If you know your net notional per currency pair facing a counterparty, you now know how to calculate the reg cap it consumes.

In Summary

• FX trades now typically consume 1.68% of notional in regulatory capital under SACCR.
• We look at how netting is applied under SACCR.
• This introduces the concepts of both Netting Sets and Hedging Sets.
• Hedging Sets can be thought of at a risk-factor level, including e.g. EURUSD in FX and EUR interest rates in Rates.
• There is no offset across Asset Classes in SACCR.
• We walk through how the Maturity Factor, Supervisory Factor and Alpha are applied to SACCR portfolios.