Background
In March 2014, the Basel Committee on Banking Supervision published bcbs279, the Standardised Approach for measuring Counterparty Credit Risk exposures. SA-CCR replaces the current non-internal model approaches, the Current Exposure Method (CEM) of 1995 and the Standardised Method (SM) of 2005. The majority of banks currently use CEM as relatively few firms have Internal Model Method (This blog looks at IMM dates in detail.”>IMM) approval from their regulator. As SA-CCR is (slowly) implemented by national regulators over the coming years, this new approach to measuring exposures will have an impact on credit risk capital and leverage ratio calculations.
Bottom-Up
For this blog, I would like to go into the details of the 8 (ish) steps required to implement the calculations involved to measure the “Exposure at Default” under SA-CCR for Rates products. Our headline equation looks fairly innocuous:
EAD = Alpha * (Replacement Cost + Multiplier * AddOn)
Where Alpha is defined as 1.4. But to get there we need to translate trade-level economic details to match the terms above. According to my reckoning, to cover all of the required calculations, the minimum information that we need regarding a given trade is:
- Currency
- Trade type (e.g. Interest Rate Swap, Swaption, Cap/Floor etc)
- Start Date of the underlying
- End Date of the underlying
- Time to Expiry (for an option, zero for linear trades)
- Notional
- Direction
- Coupon
- Break-even price (the at-the-money strike for options)
- Mark to Market
Depending on how we want to record the details of collateral agreements, the trade level details could further include:
- Cleared status
- Collateral held under the CSA
- Minimum transfer amount under the CSA
Alternatively, these CSA details could be held as a single “master” file for each CSA governing a relationship with your counterparty. These aspects are fairly trivial from the point of view of the equations themselves so we won’t dwell on them.
The key point to understand is that, unlike ISDA SIMM, a simple Delta/Vega ladder of your exposures to your counterparty will not be enough to perform the calculations required under SA-CCR.
Step One – Date Calculations
We must define the following terms. All are measured in years:
\( S_{i} \)= Time to start period
For typical Interest Rate Swaps, this is zero. For Forwards it is the start date of the swap. For Options, this is the time to expiry of the option.
\( M_{i} \)= Maturity of the swap
For Interest Rate Swaps, this is the time from the start date to maturity. For physically settled options, this is the length of the underlying swap. For cash-settled options, it is the time to expiry.
\( E_{i} \)= Time to final maturity
For Interest Rate Swaps, this is the same as \(M_{i}\). For Options, this is the sum of \(M_{i}\) and \(S_{i}\).
\( T_{i} \)= Time to final option expiry
For Bermudan Swaptions, this is hence the final exercise date.
The table on page 10 of bcbs279 provides enough details to deal with all of the permutations I can think of. Let us know if you think there are any grey areas….
Step Two – Trade Level Adjusted Notional
Now that our trades are adequately described, we can move forward with some calculations regarding the risk of a trade. First, we must consider adjusting the trade notional according to the following equation:
\( \tag {1} d_{i} = TradeNotional * \frac{exp(-5\% * S_{i}) – exp(-5\% * E_{i})}{5\%}\)For interest rate swaps that have already started, we are simply taking “e” to the power of a negative multiplier of 5%. Hence the effective multiplier to the trade notional increases as maturity increases. For swaptions, we are taking the difference between “e” raised to this number and the time to expiry. So for short dated options, it is a very similar multiplier to the underlying swap itself.
Step Three – Calculate Delta, δ
For all products without any optionality, δ is equal to one. However, for all option positions we must calculate the value of δ. This is straightforward, following the equations set out below:
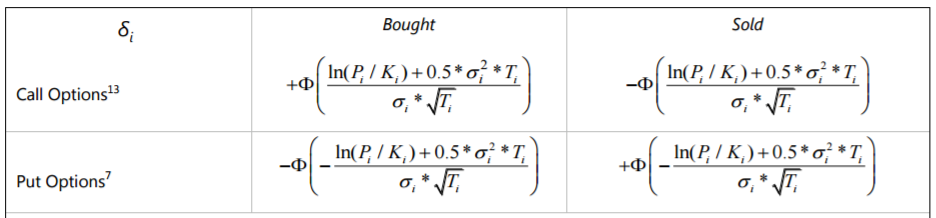
The terminology used is relatively “industry-standard” here. In summary, we are taking the value of the standard normal distribution function (excel function “NORMSDIST” can replace the greek letter “Phi” φ in the above) of the ratio between the ATM and the strike price, multiplied by a ratio of volatility and time to final expiry.
The volatility, σ, to use is 50% for Interest Rates. This is defined in a look-up table on page 19 of the bcbs279:
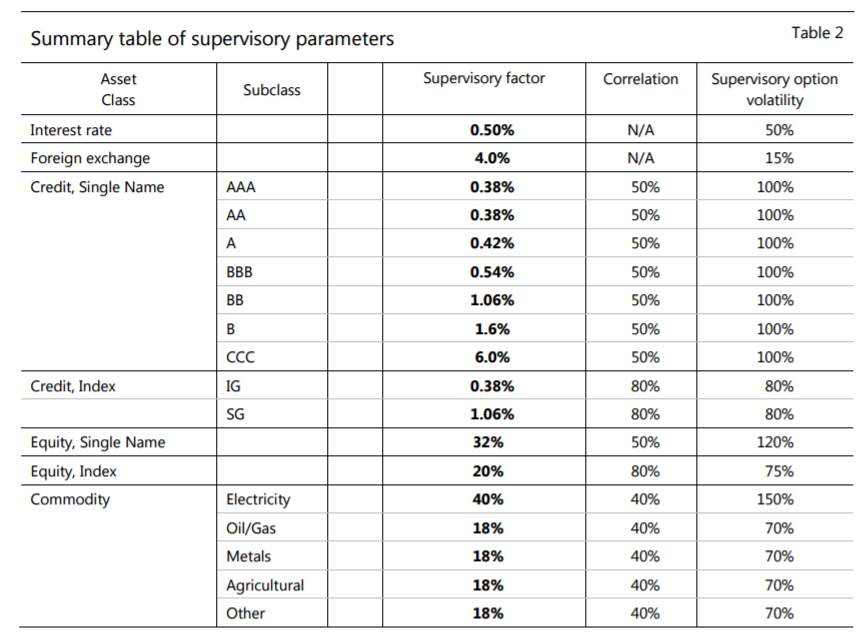
It is interesting to note that only a single factor applies for all Rates derivatives. No distinction between maturities, currencies etc.
Step Four – Calculate Risk Horizon
We now need to calculate \( Mf_{i}\). I choose to do this at a trade level as it makes data aggregation easier later on. For unmargined trades longer than one year, this is 1. Otherwise it is;
\( \tag {2} Mf_{i} = \sqrt \frac {min(M_{i};1)}{1} \)For Margined transactions, the function is of the same form, but the periods to use are very prescriptive, depending on the MPOR;
\( \tag {3} Mf_{i} = \frac{3}{2} \sqrt \frac {MPOR}{1} \)As Amir explained in his SA-CCR blog, the MPOR is either 5 days for cleared transactions or a minimum of 10 days for bilateral swaps – even with daily collateral calls. This equation alone therefore gives us a nice feeling for how beneficial clearing is under the SA-CCR world. Changing from uncleared to cleared for a 10 year swap changes this \( Mf_{i}\) term from 1 to 0.3. A nice 70% reduction.
Let’s therefore look at how this \( Mf_{i}\) term is incorporated into the overall calculations.
Step Five – Calculate Trade Level Exposure at Default
We now simply multiply the results of Steps 2, 3, and 4 together:
\( \tag {4} D_{i} = δ_{i} * Mf_{i} * d_{i}\)i.e. our trade level contribution to the exposure at default is the adjusted notional amount, multiplied by the delta and then by the scaling factor for the margin period of risk. Fairly simple really. Thankfully, paid positions are shown as positive and received positions as negative, consistent with the trading community.
Step Six – Aggregate Across Maturities
We now aggregate these values of \( D_{i}\) at a currency level. Each trade is grouped into either a sub-one year, 1-5 year or 5 year plus maturity bucket. The values of \( D_{i}\) are summed together within each maturity bucket, and then aggregated across maturities according to the following:
\(\tag {5} EffectiveNotional_{CCY} = \sqrt {[D_{1}^2 +D_{2}^2+D_{3}^2 + 1.4*D_{1}*D_{2} + 1.4*D_{2}*D_{3} + 0.6*D_{1}*D_{3}]}\)Our eagle-eyed readers will no-doubt recognise the similarity of this equation with those we implement for ISDA SIMM and FRTB…
Step Seven – Calculate Add-On for Rates
Armed with each “Effective Notional” calculation by currency, we now revert to “Table 2” above and look up the Supervisory Factor for Rates – equal to just 0.5%. We multiply the \( EffectiveNotional\) by 0.5% and the sum is equal to our AddOn for Rates.
Step Eight – Exposure at Default
Finally, we can look at the Replacement Cost and Multiplier for our final calculations. In practice, RC will typically be zero in a post-UMR world where zero threshold, daily collateralised agreements are (trying) to be market standard. And the multiplier should also be 1 under these conditions. You can check out Amir’s previous blog for the intricacies around these two values.
Therefore, our final equation started out as;
EAD = alpha * (Replacement Cost + multiplier * AddOn)
where-as in reality, Alpha is set by the regulators at 1.4, Replacement Cost will be zero and the multiplier will be 1. Therefore, when considering SA-CCR, we are really considering:
Exposure At Default = 1.4 * (AddOn)
For those of you interested, all of these calculations fit rather neatly onto a single sheet of Excel:
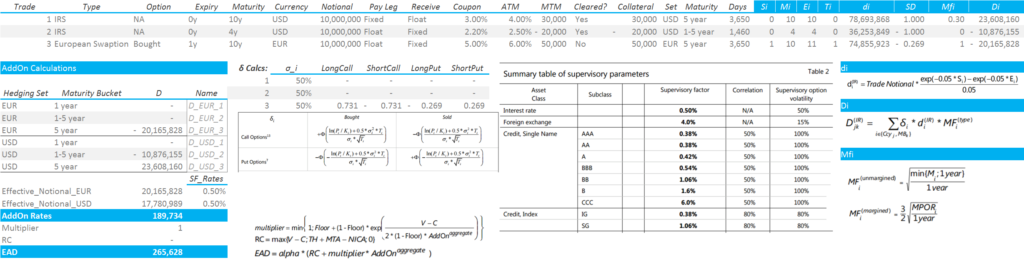
In Summary
- Trade-level primary economic details are required to calculate capital requirements under SA-CCR.
- The calculations involved are fairly intricate but simple to replicate.
- To understand SA-CCR, in today’s post-UMR world, we only need to understand the inputs to the AddOn calculation.
- This is still a notional-based measure.
- Full netting of exposures is allowed within a single maturity bucket of the same currency.
- Understanding the calculations is the first step towards measuring the impact of these new regulations.
- In future blogs we will study the effect of moving from CEM to SA-CCR for some simple portfolios.
- UPDATE: We now offer free 14-day trials for our SA-CCR for Excel product

Do cross-currency interest rate swaps go into the IR or FX category, or (possibly) both?
Hi Stuart. This is a great question and had me scratching my head. I did eventually find footnote 14 on page 13 of bcbs279: