In my recent article, Swaps Compression and Compaction on trueEx and Tradeweb SEFs, I looked at the mechanics of these trades, the evidence in SEF and SDR figures and stated that the benefit was to reduce line items and clearing fees.
In this article, I am going to take a deeper look at just the impact of compression on clearing fees and margin. In order to determine whether the cost-benefit in terms of fees and margin is a positive factor or not on the benefit of reducing portfolio complexity by removing line items.
Client Clearing Fees
For Clients the first set of fees are those charged by their FCM or Clearing Broker.
Such fees typically consist of a new trade ticket fee, a periodic maintenance fee and a portfolio charge. The latter being for the funding cost implications of a segregated account, financial resource utilisation and funding of default fund contributions.
The most convenient public disclosure on OTC Clearing Fees is that required by EMIR and on the assumption that such fees are similar to those charged to US firms under Dodd-Frank, lets see what a few of these state:
- Barclays Fees, £750 per new trade, £75 per quarter, 100 bps on Initial Margin
- JP Morgan Fees, $1,500 per trade, 60 bps on Initial Margin
- Citi Fees, $750 per trade, 50 bps on Initial Margin
Our list of three show a wide variation in list prices, however we can be sure that after negotiation actual prices will converge; provided a minimum annual revenue threshold of around $250,000 is met.
Lets assume a client can negotiate a $500 per ticket fee and 60 bps on IM.
Clearing House Fees
Clearing House fees are passed on by FCMs to Clients and there are two types of plans; a standard one and a high turnover one.
Standard Plans:
- CME OTC IRS, fees are $0.25-$24 per million for a trade and then $2.00 per million per annum per line item and volume discounts
- LCH SwapClear, fees are $0.9-$18 per million for a new trade and then $3.00 per million per trade per annum.
High Turnover Plan:
A client not only has the funding cost of the Initial Margin requirement, but as we see above the clearing fees also have a component linked to the IM. Consequently IM is an important and significant determinant of the overall cost.
Compression – A Simple Example
Lets now looked at a worked example of compression costs and savings in action.
Assume we just have a single 2Y Swap of $100 million receive fixed in our portfolio, which we executed one week ago and that we now no longer need.
What is the cost of the compression?
Well as we know from my prior blog, this involves entering into a new swap with the same terms but opposite direction (pay fixed) to the existing swap.
- Lets first assume there is no explicit execution fee (not un-reasonable?), so we are left with Clearing and SDR reporting costs
- Consequently we need to pay $500 for client clearing fees and $250 for CME or $225 for LCH (assuming the standard plan)
- For SDR reporting, lets assume $15 per trade
- So $765 for CME and $740 for LCH
- Lets call this $750
And what is the saving?
- Well firstly we will not have to incur the annual Clearing House charge of $200 for CME or $300 for LCH.
- Which for two years is $400 or $600 respectively.
- Secondly we no longer have an IM requirement as the net risk of the two trades is zero.
- Which means that we no longer need to fund the IM requirement and will not have to pay 60bps on IM to our FCM
- So the saving is either $400 or $600 plus the reduction in funding cost plus IM fee saving.
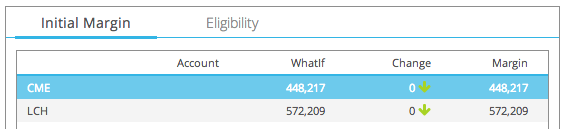
To proceed we need to determine the IM for our 2Y Swap, which we do in CHARM as below:
Then for arguments sake lets assume our funding rate is 2% more than the interest we earn on the margin deposit.
So our monthly funding cost is $750 for CME and $950 for LCH, at least for the first month.
After that IM decreases as our 2Y Swap ages, mainly as DV01 decreases with remaining maturity (a 1Y Swap has less than half the DV01 of a 2Y). As a rough approximation lets assume that the average IM over the life of our 2Y Swap is 40% of the IM at inception. Our funding cost over 2Y is then $7,200 for CME and $9,000 for LCH.
Using the same 40% assumption for average IM over the 2Y, we can also estimate the 60bps per annum of IM as $5,400 for CME and $6,800 for LCH.
Bringing all the above figures together:
- Cost of compression trades is $750
- Benefit over the 2 years is $13,000 for CME and $16,500 for LCH
So very clearly in this case the cost-benefit of compression is firmly in the positive.
However in this simple example, given that the DV01 of the 2Y trade is approximately $20,000, the business imperative to neutralise this DV01 is of more importance than the cost benefit of compression.
Consequently the decision to do compression is not determined by the cost-benefit of compression per se, but simply the use of compression to neutralise the DV01.
Compression – Another Example
Lets now construct another example, one in which we have already decided to hedge the original Swap, one-week later with a new 2Y swap (on-the-run and par) and are now left with two Swaps with a small difference in fixed rate (e.g. 0.1 bps) and a 1-week mis-match in maturity dates.
We could chose to let these trades run down to maturity.
However lets see whether compression is also worth-while in this case.
Cost of compression:
- Enter into two trades to off-set the two existing ones
- So $1,000 in Client Clearing Fees and $500 for CME or $450 for LCH
- For SDR reporting, lets assume $15 per trade, so $30 in total
- A total of $1,530 for CME and $1,480 for LCH
- Lets call this $1,500
Saving:
- No annual maintenance charge for the two trades
- So $800 for CME or $1,200 for LCH
- Reduction in funding cost and IM fee?
In this case the reduction in funding costs is much less significant, simply because the 2 original trades are already almost but not quite perfectly hedged; except for 0.1 bps on fixed rate and 1-week maturity mis-match.
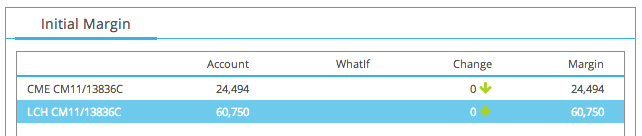
In-fact if we construct an account with these two original trades in and run in CHARM, we get the following:
So we can see that there is still in-fact a small Initial Margin, much less than than we had before, but material nonetheless.
The funding cost of this (using the same 2% and 40%) over the 2 years is then $400 for CME and $970 for LCH.
And the 60 bps of IM over 2 years is, $300 for CME and $700 for LCH.
Bringing all the above figures together:
- Cost of compression trades is $1,500
- Benefit over the 2 years is $1,100 for CME and $2,300 for LCH
So in this case for CME the cost-benefit is not positive, while for LCH it still is.
However if we were not on a standard plan but a high-turnover plan, our cost of compression would be just $1,100 as the Clearing House fee would be $25 and the 10bps on IM.
This moves the cost-benefit towards positive territory for CME.
As would a greater mis-match than 1-week and a greater difference than 0.1 bps.
So we can see that even with seamingly hedged portfolios, there is a cost-benefit in compression to get rid of the residual risk.
Compression – A Portfolio Example
Now in a real-world we would not be looking at simple portfolios with just our 2Y Swap trade but a portfolio with many existing trades.
In this case compression to reduce line items in itself would generate significant savings in the Clearing House maintenance charge (and even more potential savings if our FCM also charges this, as Barclays state in their document above).
Lets say we had 100 line items with gross notional of $5 billion, an average size of $50 million per trade.
The annual maintenance for these would be $10,000 for CME and $15,000 for LCH, not massive but sill adds up over the life of these trades which maybe 5Y or 10Y or 30Y.
While the reduction in Initial Margin, should be determined as the marginal impact on the portfolio margin of the compression trades.
A more involved calculation, but one that can be performed in CHARM by loading the existing portfolio and a what-if list of compression trades.
I won’t go into the details of this now, except to note that in some cases it may not be a reduction but an increase in margin and so not a saving but a cost! (If you are interested in details on the portfolio example, please send me an email).
For a compaction, where we are seeking to not change the risk (or the margin) there would be no reduction in margin. So in this case the focus is simply on the clearing fees, both the new trade fees and the reduction in annual maintenance fees.
Thats its for today, very detailed, so thank you for sticking with it.
Any errors in the above calculations are all mine, so please let me know if you find any.
Summary
Compression trades have a cost as they are new trades that must be cleared.
The cost is in Client Clearing fees per trade paid to the FCM and Clearing House fees.
The reduction in line items, reduces portfolio complexity is often the prime reason for compression.
This article looks specifically into clearing fees and margin reduction.
While the new compression trades attract a new trade clearing fee, the fact that they net down (extinguish) the existing trades mean that there is no longer an annual maintenance fee payable to the Clearing House
The greater the number of trades (line items) removed, the greater this benefit.
Another benefit, often greater, is the reduction in Initial Margin .
As this determines both funding cost and the FCM portfolio charge.
A simple example of a single trade above show’s how to calculate the cost-benefit.
Another example showing compression on a hedged portfolio is also shown.
A real-word portfolio calculation is too lengthy for this article, but may be performed using CHARM.