- The final piece of the LIBOR-cessation puzzle is about to be completed.
- We’ve previously looked at how RFRs can be used to replace a range of ‘IBOR indices.
- Now we look at the exact parameters that will be used to calibrate the ‘IBOR- RFR spreads.
Historic Calibration
Market consultations from ISDA have led to the “compounding in-arrears” methodology being used to replace LIBORs with RFRs in the event of a LIBOR ceasing publication.
On top of that compounded calculation, the long-run difference between LIBOR (risky, credit) with RFRs (near risk free, some are secured) will be calibrated versus some sort of historic average.
What Average Will be Used?
The purposes of the current ISDA consultation is therefore to decide:
- What look-back period should be used? 1 year? 5 years? 10 years? etc.
- What averaging methodology should be used? Median, mean, trimmed mean – any others?
Mean vs Median
Let’s start with the averaging methodology. In response to prior consultations ISDA received the following responses:
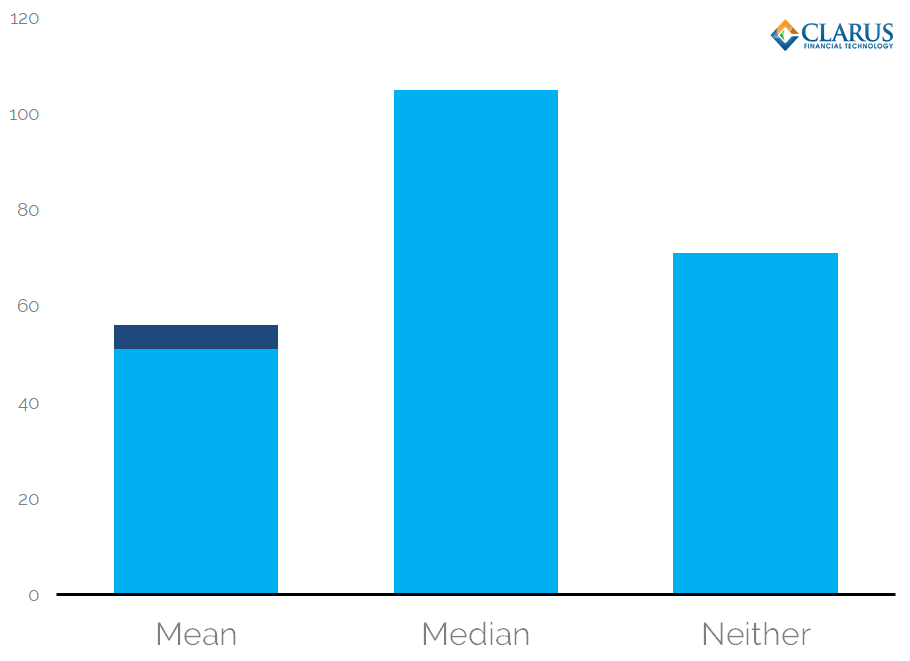
Showing;
- The strongest level of support is for a Median methodology.
- Ambivalence (neither) outweighed a mean even allowing for those of us who support a Trimmed Mean.
For anyone who has traded any basis, a strong motivation to hedge the risk is the presence of tail events. A median would ignore these tail events, which ignore the economic reality of why trading occurs in these products. A mean gives equal weighting to tail events, which is probably unfair. For those reasons, Clarus were amongst the respondents in support of a Trimmed Mean. We believe this to be the most economically fair result and we anticipate that it will minimise value transfer.
However, it pays at this point to fast forward to question 7 of this current consultation, that asks:
If outliers were to be excluded, to what extent should the data be trimmed? For example:
Consultation on Final Parameters for the Spread and Term Adjustments in Derivatives Fallbacks for Key IBORs
– the top one percent and bottom one percent of the observations could be removed for the calculation;
– a winsorized mean could be used, pursuant to which observations that are in the top one percent could be set to the 99th percentile value and observations that are 12 in the bottom one percent could be set to the 1 st percentile value for the calculation;
– the maximum and minimum could be removed for the calculation; or
– only observations within +/- three standard deviations could be used for the calculation.
Should trimming be symmetric (i.e., trimming the same proportion of observations from both tails of the distribution) or asymmetric (i.e., one tail of the distribution should be trimmed more than the other)?
This question highlights some of the difficulties we may face in agreeing a consensus for the trimming mechanism. Or it might just be complicating things!
When looking at our work on GBP Spreads, it is not that unusual for the spread to be negative for a short period of time. This is further covered in questions 8 and 9:
8. If negative spreads have been historically observed for an IBOR/RFR pair, are there compelling reasons to exclude such observations from the calculation of the spread adjustment? If so, what are they?
Consultation on Final Parameters for the Spread and Term Adjustments in Derivatives Fallbacks for Key IBORs
9. Negative spreads can be prevalent for some IBORs. If negative spreads have occurred frequently enough that the spread adjustment is itself negative, are there compelling reasons to not implement a negative spread adjustment?
We think that both negative and positive outliers should be trimmed and we were considering something more like the middle 75% of observations.
More on Trimming
Whilst we support a Trimmed Mean, it is worth noting from a pragmatic point of view that the methodology used for trimming may not be all that material. For example, below is the five year history of the 1m GBP Libor spread. It looks pretty volatile, with periods in negative territory.
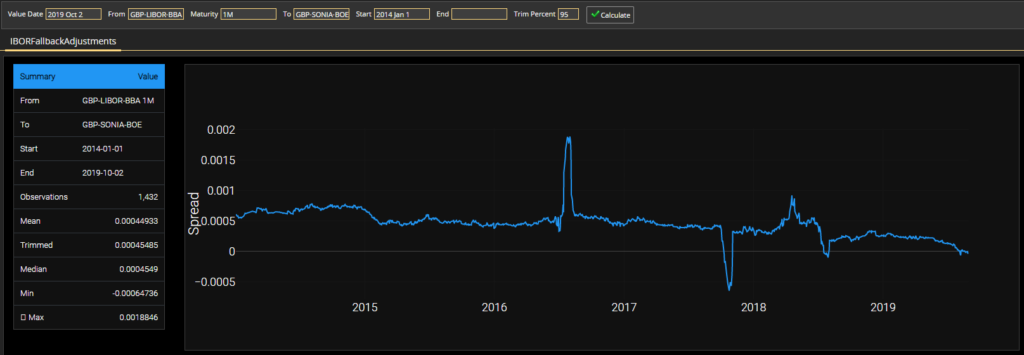
I thought that a trimmed mean would therefore show some stark differences. In reality, it really doesn’t!
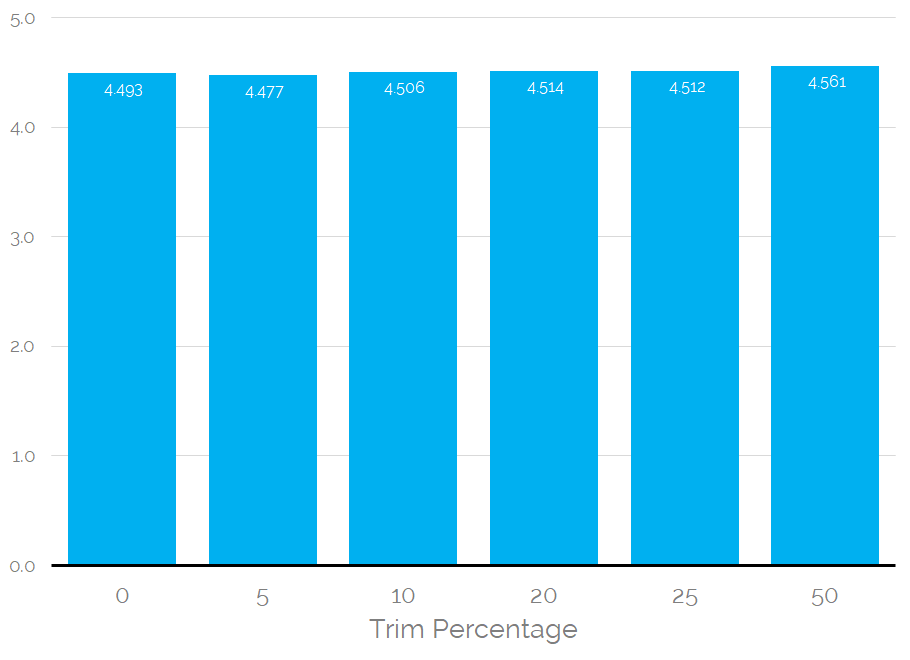
Showing;
- The calibrated Trimmed Mean for trim percentages ranging from 5% (i.e. the middle 95% of observations are used) up to 50%.
- The Mean hardly changes. The above values are expressed in basis points, so we are talking about changes in the hundredths of a basis point here.
- I think the industry should recognise that the exact trimming methodology is unlikely to end up being material, particularly when you consider that the 2008 stress period is extremely unlikely to form part of the lookback period (see below).
- I realise we are talking about potentially huge positions, but we also need some pragmatism here.
Lookback Period
In response to prior consultations, ISDA received the following responses:
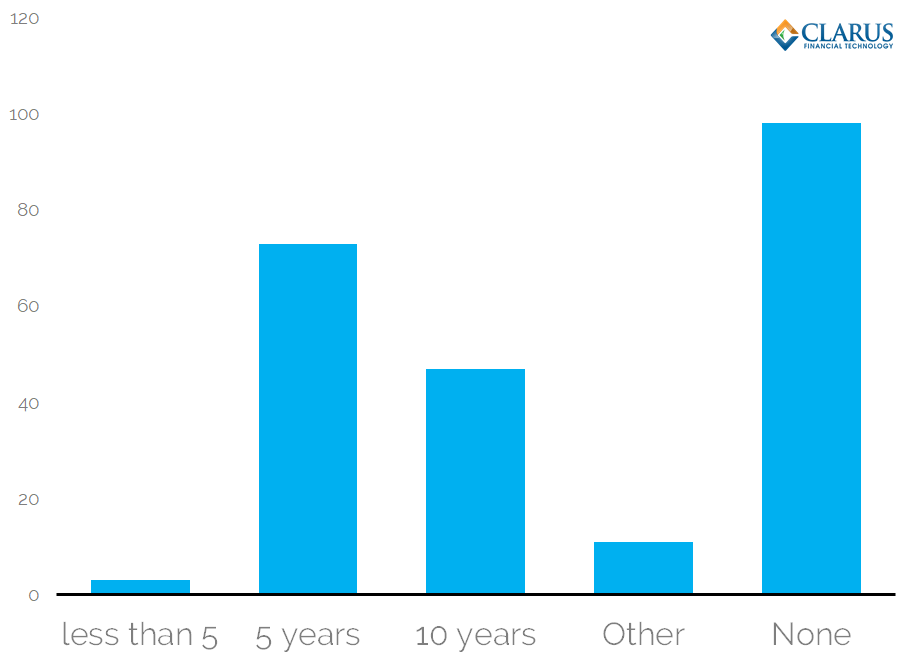
Collated responses across 2018 and 2019 prior consultations.
Showing;
- Ambivalence (“None” in the chart) was the most frequent response.
- 5 years (or lower) received more support than 10 years.
- We should note that neither 5 nor 10 year lookback periods will include 2008.
The argument for a short lookback period can be guided by the idea that current market conditions have all of the relevant data baked into them, therefore are the most accurate representation of the “true basis”. This is pretty compelling when you think of the structural changes (regulations) that have come into play over the past ten years – are observations from 2011 really relevant now?
Choose One!
This consultation serves to highlight the rabbit hole that the industry could end up going down if we get bogged down with too many options on the table. ISDA have fortunately narrowed the consultation down to two approaches:
- Median over five years.
- Trimmed Mean over 10 years (trimming methodology to be decided at a later date).
Given the level of ambivalence previously (36% of respondents could be considered ambivalent), it looks like median over five years may win the day.
I am still in the Trimmed Mean camp, not least because the Median will prove to be very sticky, even if we see a fundamental change in realised basis over the next two years. That does not sit comfortably with me.
Whatever your thoughts, now is the time to speak up and come out of the ambivalence camp!
Wait, there is a little bit more…
Mirroring the work that the Swiss Working Group has done (and I am sure the other national working groups too), there is a whole section at the end of this consultation on whether we should use backward shift or a lock-out period to deal with inevitable requests for payment delays.
I think responses will likely be in the ambivalence camp here, but those who do respond are very unlikely to choose the lock-out. I guess we just need to consult the market to ensure that no one really wants to change the fundamental economic observation period and decide which banking days should be used to calculate the so-called “backward shift”.
In Summary
This is hopefully the final consultation on IBOR fallbacks.
The industry needs to choose between two options for the historic calibration of RFR vs IBOR spreads. Those are:
- Median over five years.
- Trimmed Mean over 10 years (trimming methodology to be decided at a later date).
We recognise that it takes a lot of time, effort, resources and brain power to respond to these consultations. But it is an important effort so that the industry makes the right decisions.
Therefore, hopefully for the last time, we encourage all of our readers to respond to this important part of the puzzle.

Thanks for your excellent work Chris.
ISDA fallbacks are an unholy mess. We are being asked to determine a spread by voting for one of two options, and many of those voting will have considerable economic exposures to the level of this spread. The two options don’t even measure the thing we are trying to opine on (the credit spread). And we don’t even know yet how we are going to calculate the realised rate to apply this adjustment spread to.